problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
7.1. Find the smallest natural solution of the inequality $2^{x}+2^{x+1}+\ldots+2^{x+2000}>2^{2017}$. Answer. 17. | Solution. The value $x=17$ is clearly a solution. If $x \leqslant 16$, then we have
$$
2^{x}+2^{x+1}+\ldots+2^{x+2000} \leqslant 2^{16}+2^{17}+\ldots+2^{2015}+2^{2016}<2^{2017}
$$
since this inequality reduces sequentially to the following: $2^{16}+2^{17}+\ldots+2^{2015}<$ $2^{2017}-2^{2016}=2^{2016}, 2^{16}+2^{17}+\ldots+2^{2014}<2^{2016}-2^{2015}=2^{2015}, \ldots, 2^{16}+2^{17}<2^{19}-2^{18}=2^{18}$, $2^{16}<2^{18}-2^{17}=2^{17}$, which is true. | 17 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
2. First-grader Petya was laying out a contour of an equilateral triangle with the tokens he had, so that each of its sides, including the vertices, contained the same number of tokens. Then, with the same tokens, he managed to lay out the contour of a square in the same way. How many tokens does Petya have, if each side of the square contains 2 tokens less than each side of the triangle? | Answer: 24.
Solution. Let the side of the triangle contain $x$ chips, and the side of the square - $y$ chips. The total number of chips, counted in two ways, is $3 x-3=4 y-4$ (we account for the corner chips being counted twice). From the problem statement, it follows that $y=x-2$. Therefore, we get the equation $3(x-1)=4(x-3)$, from which $x=9$. Thus, the total number of chips is $3 \cdot 9-3=24$. | 24 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Petrov and Vasechkin were solving the same arithmetic problem. A certain number had to be divided by 2, multiplied by 7, and 1001 subtracted. Petrov performed all the operations correctly, while Vasechkin got everything mixed up: he divided by 8, squared the result, and also subtracted 1001. It is known that Petrov got a prime number. What number did Vasechkin get? | Answer: 295.
Solution. Note that the number 1001 is divisible by 7 without a remainder. This means that the number Petrov obtained must be divisible by 7. But it is a prime number, so Petrov got 7. Let's reverse the operations Petrov performed and find the original number: $\frac{7+1001}{7} \cdot 2=288$. Now, let's repeat Vasechkin's operations with it: $(288: 2)^{2}-1001=295$. | 295 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. The numbers from 1 to 8 are arranged at the vertices of a cube such that the sum of the numbers in any three vertices lying on the same face is at least 10. What is the smallest possible sum of the numbers at the vertices of one face? | Answer: 16.
Solution. Each face has a vertex where a number not less than 6 is placed. Indeed, otherwise, one of the triples of the remaining largest numbers $2,3,4,5$ would give a sum less than 10 (specifically, the triple $2,3,4$ with a sum of 9).
Consider a face containing the vertex where the number 6 is placed. Since the sum of the numbers in the other three vertices is not less than 10, the sum of all numbers in the vertices of this face is not less than 16.
An example of an arrangement where the smallest sum of numbers in the vertices of one face is 16 is shown in the figure: the sum of the numbers in the
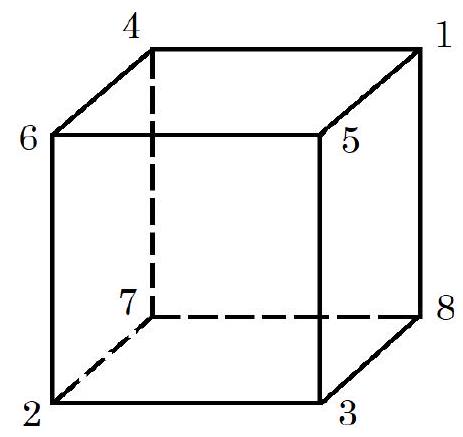
front face is $2+3+5+6=16$. | 16 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
7. All natural numbers, the sum of the digits of each of which is equal to 5, were arranged in ascending order. What number is in the 125th place?
Otvet: 41000. | Solution. Let's calculate the number of $n$-digit numbers, the sum of the digits of each of which is equal to 5, for each natural $n$. Subtract 1 from the leading digit, we get a number (which can now start with zero), the sum of the digits of which is equal to 4. Represent the digits of this number as cells, in each of which there is a number of balls equal to the digit in the corresponding place. Distributing 4 balls into $n$ cells is the same as placing $n-1$ partitions between 4 balls (there may be no balls between some partitions). This can be done in $C_{n+3}^{4}=\frac{(n+3)(n+2)(n+1) n}{24}$ ways, which is also the number of the sought $n$-digit numbers.
For $n=1,2,3,4,5$ we get respectively $C_{4}^{4}=1, C_{5}^{4}=5, C_{6}^{4}=15, C_{7}^{4}=35, C_{8}^{4}=70$, totaling 126 numbers. The number 50000, the largest five-digit number of this kind, stands at the 126th place. Therefore, the previous one, 41000, stands at the 125th place. | 41000 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5.1. For the sequence $\left\{a_{n}\right\}$, it is known that $a_{1}=1.5$ and $a_{n}=\frac{1}{n^{2}-1}$ for $n \in \mathbb{N}, n>1$. Are there such values of $n$ for which the sum of the first $n$ terms of this sequence differs from 2.25 by less than 0.01? If yes, find the smallest one. | Answer: yes, $n=100$.
Solution. The general formula for the terms of the sequence (except the first) can be written as $(n \geqslant 2)$:
$$
a_{n}=\frac{1}{n^{2}-1}=\frac{1}{2}\left(\frac{1}{n-1}-\frac{1}{n+1}\right)
$$
As a result, the sum of the first $n$ terms of the sequence, except the first, takes the form:
$$
\begin{aligned}
& \frac{1}{2}\left[\left(1-\frac{1}{3}\right)+\left(\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{3}-\frac{1}{5}\right)+\left(\frac{1}{4}-\frac{1}{6}\right)+\left(\frac{1}{5}-\frac{1}{7}\right)+\right. \\
& \left.\quad+\ldots+\left(\frac{1}{n-3}-\frac{1}{n-1}\right)+\left(\frac{1}{n-2}-\frac{1}{n}\right)+\left(\frac{1}{n-1}-\frac{1}{n+1}\right)\right]
\end{aligned}
$$
After simplifications, for the sum of the first $n$ terms of the sequence, we can write:
$$
S_{n}=1.5+\frac{1}{2}\left[1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1}\right]=2.25-\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)
$$
Let $f(n)=\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)$. Then since $f(n)$ is decreasing and
$$
\begin{aligned}
f(100) & =\frac{1}{2}\left(\frac{1}{100}+\frac{1}{101}\right)\frac{1}{2}\left(\frac{1}{100}+\frac{1}{100}\right)=\frac{1}{100}
\end{aligned}
$$
the desired value of $n$ is 100. | 100 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. Can non-negative integers be placed on the faces of two cubes so that when they are randomly thrown, the sum of the points showing can be equal to any divisor of the number 36? If this is possible, indicate the sum of all 12 numbers on the faces; if it is impossible - indicate 0. | Answer: The sum is 111. Solution. The numbers $1,2,3,4,5$ and 6 can be placed on the faces of one die, and $0,6,12,18,24,30$ on the faces of the other. Then the sum of the points rolled can be equal to any of the numbers from 1 to 36. The sum of the numbers on all faces is 111. This sum does not depend on how the dice are marked. Since the sum from 1 to 36 is 666, the average (expected value) is $666 / 36=18.5$. On the other hand, the average can be calculated for each die separately, resulting in $S_{1}+S_{2}=111$. | 111 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Find all three-digit numbers $\overline{L O M}$, composed of distinct digits $L, O$ and $M$, for which the following equality holds:
$$
\overline{L O M}=(L+O+M)^{2}+L+O+M
$$ | Answer: 156. Instructions. Let $x=L+O+M$. Then $\overline{L O M}=x(x+1)$. In this case, $x \geq 10$ (otherwise $x(x+1)<100)$ and $x \leq 24$ (the sum of digits does not exceed $9+8+7=24$). Therefore, $x \in[10 ; 24]$. From the relation $100 \cdot L+10 \cdot O+M=x^{2}+L+O+M$ it follows that $x^{2}=99 \cdot L+9 \cdot O$, which means $x$ is divisible by 3. It remains to substitute the values $12,15,18,21$ and 24 into $x(x+1)$ and check the sum of the digits of the resulting number. It matches $x$ only when $x=12$. | 156 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Pete was given a new electric jigsaw for his birthday, with a function to count the length of the cuts made. To try out the gift, Pete took a square piece of plywood with a side of $50 \mathrm{cm}$ and cut it into squares with sides of 10 cm and squares with sides of 20 cm. How many squares in total were obtained, if the electric jigsaw shows a total length of cuts of 2 m $80 \mathrm{cm}$? | Answer: 16. Solution. Each protruding edge is part of the perimeter of two figures, in addition, the perimeter of the original square must be taken into account, from which we get that the total perimeter of the resulting small squares is $280 \cdot 2+200=760$. Now we can denote the number of squares through $x$ and $y$ respectively and solve the system $\left\{\begin{array}{c}10^{2}-x+20^{2}-y=50^{2}, \\ 4-10-x+4 \cdot 20-y=760,\end{array}\right.$, or follow the following reasoning. If all the squares had a side of 10, there would be $6 \mathbf{~} 25$ pieces, then the total perimeter would be $25 \cdot 40=1000$. If we replace four small squares $10 \times 10$ with a square $20 \times 20$, the perimeter will increase by $160-80=80 \mathrm{cm}$. To get 760 from 1000, this needs to be done 3 times. This means there will be 3 squares 20x20 and 13 squares 10x10 - a total of 16 squares. | 16 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. How many four-digit numbers exist that have the following properties: all digits of the number are even; the number is divisible by four, if the last digit is erased, the resulting three-digit number is not divisible by four? | Answer: 120. Solution. The last digit of the number must be divisible by 4 (that is, it can be 0, 4 or 8), and the second to last - not (2 or 6). In addition, the first digit is not zero. Therefore, we get $4 \cdot 5 \cdot 2 \cdot 3=120$ variants. | 120 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
2.1. [5-6.2 (20 points), 7-8.2 (15 points), 9.2 (15 points)] In how many ways can the word «РОТОР» be read from the letters in the diagram, if it is not allowed to return to the letters already passed, and readings that differ only in direction are considered the same?
| Р O Т O | дохо |
| :--- | :--- |
| O Т O P | О Х Д |
| Т O P | х О Д |
| O P | О Д |
| Р | Д | | Answer: 25.
Solution. The number of ways to read starting from the upper left letter "P" is $2^{4}=16$, as 4 steps are required to move through the letters, and each step is directed either to the right or down. If we strike out the considered letter "P", it remains to count the number of remaining ways in Fig. 1.
| O T O P | O T O | $\mathrm{T}$ | $\mathrm{T}$ |
| :---: | :---: | :---: | :---: |
| O T O P | O T O P | T O | $\mathrm{T}$ |
| T O P | T O P | T O P | T O |
| O P | O P | O P | O P |
| P Fig. 1 | $\mathrm{P}_{\text {Fig. } 2}$ | $\mathrm{P}_{\text {Fig. } 3}$ | $\mathrm{P}_{\text {Fig. }}$ |
Now, let's fix the reading direction: we will assume that the word is read such that the first letter "P" in it is not lower than the last. For the top right letter "P", we get 2 ways. Strike out this letter (Fig. 2) and consider the next letter "P". The number of ways to read starting from it is 3. Strike out this letter, as well as the letters "O" next to which no letter "P" remains, as there are no more ways to read containing these letters "O" (Fig. 3). The next letter "P" is in the same position as the previous one, so it also starts with 3 possible ways. Finally, strike it out and the "O" located above it (Fig. 4). Then only 1 way of reading remains.
In total, we get $16+2+3+3+1=25$ ways. | 25 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
7.1. [5-6.5 (а) - 20 points, б) - 20 points)] Vovochka adds numbers in a column in the following way: he does not remember the tens, and under each pair of digits in the same place value, he writes their sum, even if it is a two-digit number. For example, for the sum $248+208$, he would get the value 4416.
a) In how many cases will Vovochka get the correct answer when adding all possible pairs of three-digit numbers? (If Vovochka has already added some two different numbers in a different order previously, he does not notice it.)
б) Find the smallest possible difference between the correct answer and Vovochka's answer for all other pairs of three-digit numbers. | Answer: a) 244620 b) 1800.
Solution. a) Vovochka will get the correct answer if and only if the sum of the last and second-to-last digits also results in a digit, i.e., there is no carry-over. Let's count how many pairs of digits have a sum that does not exceed 9. If one digit is 0, the other can be any of 10 digits (any digit); if one digit is 1, the other can be 9 digits (from 0 to 8), and so on; if one digit is 9, the other can only be 1 digit (0). In total, there are $1+2+\ldots+10=55$ variants. The first digit of each of the three-digit numbers being added can be any digit from 1 to 9. Thus, we get $9 \cdot 9 \cdot 55 \cdot 55 = 245025$ variants. However, identical pairs of numbers for which Vovochka will get the correct answer are counted twice. There are $9 \cdot 5 \cdot 5 = 405$ such pairs. Therefore, Vovochka will get the correct answer in $245025 - 405 = 244620$ cases.
b) Let $\overline{abc}$ and $\overline{xyz}$ be the three-digit numbers Vovochka is adding ($a, x \geqslant 1$, since the numbers are three-digit), their sum is $100(a+x) + 10(b+y) + (c+z)$. If Vovochka got the wrong answer, then the sum of the last or second-to-last digits (or both) was a two-digit number, i.e., there are three cases.
1) If $b+y \geqslant 10, c+z < 10$, then Vovochka will get the answer $1000(a+x) + 10(b+y) + (c+z)$, and the difference between the correct answer and Vovochka's answer is $900(a+x)$.
2) If $b+y < 10, c+z \geqslant 10$, then Vovochka's answer is $1000(a+x) + 100(b+y) + (c+z)$, which differs from the correct answer by $900(a+x) + 90(b+y)$.
3) If $b+y \geqslant 10, c+z \geqslant 10$, then Vovochka will get the answer $10000(a+x) + 1000(b+y) + (c+z)$, in this case, the difference is $9900(a+x) + 990(b+y)$.
Thus, in each case, the difference between the answers will be no less than $900(a+x) \geqslant 1800$. The difference of 1800 can be obtained, for example, by adding the numbers 105 and 105: Vovochka will get the answer 2010 when the correct answer is 210. | 244620 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
13.1. [7-8.7 (20 points), 9.8 (15 points), 10.8 (20 points)] There is a rotating round table with 16 sectors, on which numbers $0,1,2, \ldots, 7,8,7,6, \ldots, 2,1$ are written in a circle. 16 players are sitting around the table, numbered in order. After each rotation of the table, each player receives as many points as the number written on the sector they end up in after the table stops. It turned out that after 13 rotations of the table, player number 5 scored a total of 72 points, and player number 9 scored a total of 84 points. How many points did player number 1 score? | Answer: 20.
Solution. Players No. 5 and No. 9 together scored $72+84=156=12 \cdot 13$ points. In one spin, they can together score no more than 12 points. Therefore, in each of the 13 spins, they together scored 12 points. Note that the 12 points they score can be one of the sums $8+4, 7+5$, $6+6, 5+7$ or $4+8$, when the sector 8 is in front of one of them or between them, i.e., in front of one of the players with numbers $6, 7, 8$. In each of these five cases, player No. 1 scores respectively $4, 3, 2, 1$ or 0 points. This can be expressed by the formula $x_{1}=\frac{x_{5}-x_{9}}{2}+2$, where $x_{n}$ is the number of points scored by the player with number $n$ in this spin. Then the number of points scored by player No. 1 after 13 spins is $\frac{72-84}{2}+2 \cdot 13=20$. | 20 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
18.1. $[10.2$ (15 points)] A wooden parallelepiped, all sides of which are expressed in whole centimeters, was painted red, and then sawn parallel to the faces into cubes with a side of 1 cm. It turned out that one third of the resulting cubes have at least one red face, while the remaining two thirds have all faces unpainted. Find the length of the parallelepiped if it is 2 cm longer than the width and 4 cm longer than the height. | Answer: 18 cm.
Solution. Let the length of the parallelepiped be $n$ cm, then the width is $n-2$, and the height is $n-4$. This gives $n(n-2)(n-4)$ cubes. The number of uncolored cubes will be $(n-2)(n-4)(n-6)$ (a layer one cube wide is "removed" from each side). This results in the equation $(n-2)(n-4)(n-7)=\frac{2}{3} n(n-2)(n-4)$ with the condition $n \geq 7$. The roots of the equation are: $n=2, n=4, n=18$. The first two roots are not valid. Therefore, $n=18$, and this is the parallelepiped $18 \times 16 \times 14$. | 18 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
20.1. [10.7 (15 points)] The function $f$, defined on the set of integers, satisfies the following conditions:
1) $f(1)+1>0$
2) $f(x+y)-x f(y)-y f(x)=f(x) f(y)-x-y+x y$ for any $x, y \in \mathbb{Z}$;
3) $2 f(x)=f(x+1)-x+1$ for any $x \in \mathbb{Z}$.
Find $f(10)$. | Answer: 1014.
Solution. If $h(x)=f(x)+x$, then from condition 2) we get $h(x+y)=h(x) h(y)$. Then, for $x=y=0$, this equality takes the form $h(0)^{2}=h(0)$, i.e., $h(0)=0$ or $h(0)=1$. In the first case, $h(x) \equiv 0$, which is impossible due to condition 1). If $a=h(1)$, then $h(x)=a^{x}$ for any $x \in \mathbb{Z}$. From condition 3), we find $a=2$, then $h(10)=2^{10}=1024, f(10)=h(10)-10=1014$. | 1014 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
20.2. The function $g$, defined on the set of integers, satisfies the conditions:
1) $g(1)>1$
2) $g(x+y)+x g(y)+y g(x)=g(x) g(y)+x+y+x y$ for any $x, y \in \mathbb{Z}$;
3) $3 g(x)=g(x+1)+2 x-1$ for any $x \in \mathbb{Z}$.
Find $g(5)$. | Answer: 248.
Solution. Let $g(1)=a$, then from condition 3) we sequentially find $g(2)=3 a-1, g(3)=$ $9 a-6, g(4)=27 a-23, g(5)=81 a-76$. From condition 2), substituting $x=4$ and $y=1$, we obtain after simplifications the equation $a^{2}-5 a+4=0$, from which $a=1$ or $a=4$. The case $a=1$ contradicts condition 1). Therefore, $a=4$, then $g(5)=81 a-76=81 \cdot 4-76=248$. | 248 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
# Task 2.
In a school test, there are 5 sections, each containing the same number of questions. Anton answered 20 questions correctly. The percentage of his correct answers was more than 60 but less than 70. How many questions were there in the test in total? | Answer: 30
Solution. According to the condition $\frac{60}{100}<\frac{20}{x}<\frac{70}{100}$, that is, $\frac{200}{7}<x<\frac{100}{3}$, so $29 \leqslant x \leqslant 33$. Since the number of questions must be divisible by 5, then $x=30$.
## B-2
In a school test, there are 4 sections, each containing the same number of questions. Anton answered 20 questions correctly. At the same time, the percentage of his correct answers was more than 60 but less than 70. How many questions were there in the test?
Answer: 32
## B-3
In a school test, there are 5 sections, each containing the same number of questions. Anton answered 20 questions correctly. At the same time, the percentage of his correct answers was more than 50 but less than 60. How many questions were there in the test?
Answer: 35
## B-4
In a school test, there are 4 sections, each containing the same number of questions. Anton answered 20 questions correctly. At the same time, the percentage of his correct answers was more than 50 but less than 60. How many questions were there in the test?
## Answer: 36
## Lomonosov School Olympiad in Mathematics
Preliminary stage $2020 / 21$ academic year for $7-8$ grades
# | 36 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
# Task 5.
Around a round table, 1001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turned out that next to each knight sits exactly one liar, and next to each liar there is a knight. What is the minimum number of knights that can sit at the table? | Answer: 502
Solution. From the condition, it follows that a knight cannot sit between two knights or two liars, and a liar cannot sit between two liars. Thus, when moving around the table, knights will be encountered in pairs, while liars will be encountered singly or in pairs. From this, it follows that each liar can be paired with a knight (and there will still be knights left who have not been paired). Therefore, the number of knights at the table is more than half of the total number of people and is also an even number, i.e., at least 502.
Example seating of 502 knights and 499 liars, satisfying the condition: first, seat 248 groups of "knight, knight, liar, liar," then three more groups of "knight, knight, liar."
## B-2
At a round table, 2001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turns out that next to each knight sits exactly one liar, and next to each liar sits a knight. What is the maximum number of liars that can sit at the table?
Answer: 999
## B-3
At a round table, 3001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turns out that next to each knight sits exactly one liar, and next to each liar sits a knight. What is the minimum number of knights that can sit at the table?
Answer: 1502
## B-4
At a round table, 4001 people are sitting, each of whom is either a knight (always tells the truth) or a liar (always lies). It turns out that next to each knight sits exactly one liar, and next to each liar sits a knight. What is the maximum number of liars that can sit at the table?
Answer: 1999
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary Stage 2020/21 academic year for grades 7-8
## B-1
# | 502 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
# Problem 6.
Find the smallest natural number $n$, for which the number $n+2018$ is divisible by 2020, and the number $n+2020$ is divisible by 2018. | Answer: 2034142
Solution. By the condition $n+2018=2020 m, n+2020=2018 k$, hence $1009 k-1010 m=1$. The solution to this Diophantine equation is: $k=-1+1010 p, m=-1+1009 p$. Therefore, $n+2018=$ $2020(-1+1009 p)=-2020+2020 \cdot 1009 p$, from which $n=-2018-2020+2020 \cdot 1009 p$. The smallest natural $n$ is $n=2020 \cdot 1009-2020-2018=2034142$.
## B-2
Find the smallest natural number $n$ for which the number $n+2019$ is divisible by 2020, and the number $n+2020$ is divisible by 2019.
Answer: 4074341
## B-3
Find the smallest natural number $n$ for which the number $n+2019$ is divisible by 2021, and the number $n+2021$ is divisible by 2019.
Answer: 4076359
## B-4
Find the smallest natural number $n$ for which the number $n+2020$ is divisible by 2022, and the number $n+2022$ is divisible by 2020.
Answer: 2038178
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary stage $2020 / 21$ academic year for $7-8$ grades
## B-1
# | 2034142 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
# Problem 7.
Inside a convex 13-gon, 200 points are placed such that no three of these 213 points (including the vertices of the polygon) are collinear. The polygon is divided into triangles, with the vertices of each triangle being any three of the 213 points. What is the maximum number of triangles that could result? | Answer: 411
Solution. If each of the points is a vertex of some triangle, then the total sum of the angles will be equal to $180^{\circ} \cdot(13-2)+360^{\circ} \cdot 200=180^{\circ} \cdot(11+400)=180^{\circ} \cdot 411$. This means 411 triangles are formed. If some points do not participate in the cutting, then the number of triangles will be less.
## B-2
Inside a convex 100-gon, 17 points are placed such that no three of these 117 points (including the vertices of the polygon) lie on the same straight line. The polygon is divided into triangles, with the vertices of each being 3 of the given 117 points. What is the maximum number of triangles that can result?
Answer: 132
## B-3
Inside a convex 200-gon, 13 points are placed such that no three of these 213 points (including the vertices of the polygon) lie on the same straight line. The polygon is divided into triangles, with the vertices of each being 3 of the given 213 points. What is the maximum number of triangles that can result?
Answer: 224
## B-4
Inside a convex 17-gon, 100 points are placed such that no three of these 117 points (including the vertices of the polygon) lie on the same straight line. The polygon is divided into triangles, with the vertices of each being 3 of the given 117 points. What is the maximum number of triangles that can result?
Answer: 215
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary stage $2020 / 21$ academic year for $7-8$ grades
## B-1
# | 411 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
# Problem 8.
Let $A(n)$ denote the greatest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9, A(64)=1$. Find the sum $A(111)+A(112)+\ldots+A(218)+A(219)$. | Answer: 12045
Solution. The largest odd divisors of any two of the given numbers cannot coincide, as numbers with the same largest odd divisors are either equal or differ by at least a factor of 2. Therefore, the largest odd divisors of the numbers $111, 112, \ldots, 218, 219$ are distinct. This means that the largest odd divisors of the numbers from $n+1$ to $2n$ are $n$ different odd numbers that do not exceed $2n$. Thus, these numbers are $1, 3, 5, \ldots, 2n-1$. If we add the number 220 to the set of numbers, the desired sum will be $1+3+5+\ldots+219-A(220)=\frac{1+219}{2} \cdot 110-55=110^2-55=12045$.
## B-2
Let $A(n)$ denote the largest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9$, $A(64)=1$. Find the sum $A(113)+A(114)+\ldots+A(222)+A(223)$.
Answer: 12537
## B-3
Let $A(n)$ denote the largest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9$, $A(64)=1$. Find the sum $A(115)+A(116)+\ldots+A(226)+A(227)$.
Answer: 12939
## B-4
Let $A(n)$ denote the largest odd divisor of the number $n$. For example, $A(21)=21$, $A(72)=9$, $A(64)=1$. Find the sum $A(117)+A(118)+\ldots+A(230)+A(231)$.
Answer: 13427 | 12045 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4.1. (13 points) A guard has detained a stranger and wants to drive him away. But the person caught said that he had made a bet with his friends for 100 coins that the guard would not drive him away (if the guard does, he has to pay his friends 100 coins, otherwise they pay him), and, deciding to bribe the guard, offered him to name a sum. What is the largest number of coins the guard can ask for so that the stranger, guided solely by his own profit, would definitely pay the guard? | Answer: 199.
Solution. If the guard asks for 199 coins, then by agreeing to give him this amount, the outsider will win the dispute and receive 100 coins. In total, he will lose 99 coins. If the outsider refuses, he will lose the dispute and lose 100 coins, which is less favorable (by 1 coin) for the one caught. If the guard demands 200, the outsider might refuse, as there is no difference in benefit. If the guard demands more, it is more advantageous for the outsider to refuse. The guard can ask for less, but the problem requires finding the largest amount. Thus, the answer is 199 coins. | 199 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
5.1. (13 points) On the picture, the entrance and exit of the maze are marked with arrows. You can move through it such that on this picture you can only move right, down, or up (you cannot turn around). How many different ways are there to navigate this maze?
---
The translation maintains the original text's formatting and structure. | Answer: 16.
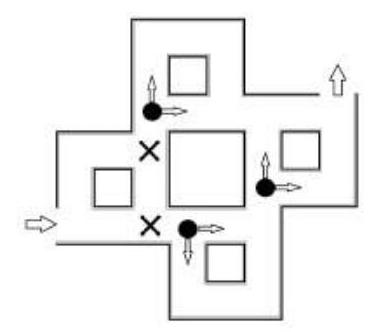
Solution. Let's call a place in the maze a fork if from it you can move in two possible directions.
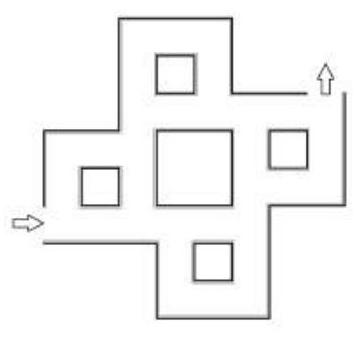
Moving up or to the right after entering, we arrive at one of the forks marked on the diagram with the symbol $\times$. From each of them to the exit from the maze, we will encounter three forks marked on the diagram with the symbol $\bullet$, so the total number of paths is $2 \cdot 2 \cdot 2 + 2 \cdot 2 \cdot 2 = 16$.
 | 16 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
8.1. (13 points) Find the smallest natural number such that after multiplying it by 9, the result is a number written with the same digits but in some different order. | Answer: 1089.
Solution. Note that the number must start with one, otherwise multiplying by 9 would increase the number of digits. After multiplying 1 by 9, we get 9, so the original number must contain the digit 9. The number 19 does not work, so two-digit numbers do not work. Let's consider three-digit numbers. The second digit (after the one) of the original number does not exceed 1, otherwise we get an increase in the number of digits. Therefore, there are only two such numbers: $\overline{1 a 9}$, where $a=0$ or $a=1$. Both numbers 109 and 119 do not meet the requirement of the problem. Let's consider three-digit numbers of the form $\overline{1 a b 9}$, where $a=0$ or $a=1$. Among them, we need to find the smallest one that satisfies the condition of the problem. But already at $a=0$ we get the number 1089, which is the answer ( $1089 \cdot 9=9801$ ). | 1089 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
9.1. (13 points) The surface of a round table is divided into 9 identical sectors, in which the numbers from 1 to 9 are written sequentially clockwise. Around the table sit 9 players with numbers \(1, 2, \ldots, 9\), going clockwise. The table can rotate around its axis in both directions, while the players remain in place. The players are seated at equal distances from each other, so when the table stops rotating, exactly one player is opposite each sector and receives the number of coins written on that sector. It is known that after 11 rotations of the table, player ㄱo4 received 90 coins, and player № 8 received 35 coins. How many coins did player № 1 receive? | Answer: 57.
Solution. If, as a result of spinning the table, one coin went to someone with numbers from 5 to 8, then player No. 8 received 5 fewer coins than player No. 9, and if one coin went to someone else, then No. 8 received 4 more coins than player No. 4. Let the number of spins where one coin went to someone with numbers from 5 to 8 be exactly $k$. Then we get the equation $-5k + 4(11 - k) = 35 - 90$, from which $k = 11$. This means that in all 11 spins, each player from 9 to 4 (if moving clockwise) received exactly 11 more coins than the previous one. Therefore, the first player has $35 + 11 + 11 = 57$ coins. | 57 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1. Several boys and girls gathered around a round table. It is known that exactly for 7 girls, the person sitting to their left is a girl, and for 12 - a boy. It is also known that for $75\%$ of the boys, the person sitting to their right is a girl. How many people are sitting at the table? | Answer: 35 people
Solution: From the condition, it is clear that there are exactly 19 girls.
Note that the number of girls who have boys sitting to their left is equal to the number of boys who have girls sitting to their right. Thus, $75\%$ of the boys equals 12, i.e., there are 16 boys in total sitting at the table. Therefore, we get 19 girls + 16 boys $=35$ people. | 35 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. Find the sum of the digits of the number $\underbrace{44 \ldots 4}_{2012 \text { times }} \cdot \underbrace{99 \ldots 9}_{2012 \text { times }}$ | Answer: 18108.
Solution: Note that $\underbrace{4 \ldots 4}_{2012} \cdot \underbrace{9 \ldots 9}_{2012}=\underbrace{4 \ldots 4}_{2012} \underbrace{0 \ldots 0}_{2012}-\underbrace{4 \ldots 4}_{2012}=\underbrace{4 \ldots 4}_{2011} 3 \underbrace{5 \ldots 5}_{2011} 6$. The sum of the digits is $4 \cdot 2011+3+5 \cdot 2011+6=18108$. | 18108 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1.1. (4 points) Mitya is 11 years older than Shura. When Mitya was as old as Shura is now, he was twice as old as she was. How old is Mitya? | Answer: 33.
Solution. 11 years ago, Shura was half as old as she is now. So, she is 22 years old, and Mitya is 33. | 33 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5.1. (13 points) Find the smallest natural number that is divisible by 11 and whose representation contains 5 zeros and 7 ones. (You can use the divisibility rule for 11: a number is divisible by 11 if the difference between the sum of the digits in the even positions and the sum of the digits in the odd positions is divisible by 11.) | Solution. The number 7 is not divisible by 2, so the number cannot have exactly $5+7=12$ digits. Let's consider the case when the number has 13 digits. If the "new" digit is zero, we again get a contradiction. Therefore, the "new" digit must be at least 1. To find the smallest number, we should place this digit as far to the right as possible in the number. Let's try to find the desired number in the form $100000111111 x$. By equating the sums of the digits in the even and odd positions, we get the equation $4+x=3$, from which $x=1$, which is impossible. Let's check the number in the form $a=10000011111 x 1$. By calculating the sums of the digits in the even and odd positions, we get $5=2+x \Rightarrow x=3$. Therefore, the desired number is 1000001111131. | 1000001111131 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
7.1. (13 points) Yura has unusual clocks with several minute hands moving in different directions. Yura calculated that the minute hands coincided in pairs exactly 54 times in one hour. What is the maximum number of minute hands that can be on Yura's clocks? | Answer: 28.
Solution. Let some two arrows coincide, then after 30 seconds they will coincide again. Therefore, the arrows in each such pair will coincide exactly 2 times per minute. Thus, if $n$ arrows move in one direction, and $m$ arrows move in the other, then $2 m n=54, m n=27$. Therefore, $n$ can be $1,3,9$ or 27. The largest sum $m+n$ is obtained when $n=1, m=27$ (or vice versa) and is equal to 28. | 28 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
9.1. (13 points) In how many ways can eight of the nine digits $1,2,3,4,5,6$, 7,8 and 9 be placed in a $4 \times 2$ table (4 rows, 2 columns) so that the sum of the digits in each row, starting from the second, is 1 more than in the previous one? | Answer: 64.
Solution. The sum of all nine numbers is 45. Let $x$ be the sum of the two numbers in the first row, and let $a$ be the one number out of the nine that we do not place in the figure. Then $x+x+1+x+2+x+3=45-a$, from which $4 x+a=39$. Since $a$ is an integer from 1 to 9, we get 2 possible cases: either $x=9, a=3$, or $x=8, a=7$.
If $a=3$, then we need to arrange the numbers $1,2,4,5,6,7,8,9$, and the sum of the numbers in the rows should be $9,10,11$, and 12, respectively. Possible options for the numbers in the first row: $9=1+8=2+7=4+5$.
If the first row contains 1 and 8, then the second row should contain 4 and 6, the third row 2 and 9, and the last row 5 and 7.
If the first row contains 2 and 7, then the second row should contain 1 and 9 (with other options, it is impossible to select numbers for the third row), the third row 5 and 6, and the last row 4 and 8.
If the first row contains 4 and 5, then the second row can have 1 and 9 or 2 and 8. But in both cases, it is impossible to find numbers for the third row.
If $a=7$, then we need to arrange the numbers $1,2,3,4,5,6,8,9$, and the sum of the numbers in the rows should be $8,9,10$, and 11, respectively. The sum of the numbers in the first row is $8=5+3=$ $6+2$.
If the first row contains 3 and 5, then the second row should contain 1 and 8, the third row 6 and 4, and the last row 2 and 9.
If the first row contains 6 and 2, then the second row can contain 1 and 8 or 4 and 5. If they contain 1 and 8, it is impossible to select numbers for the next row. Therefore, they contain 4 and 5, then the next row contains 1 and 9, and the last row 3 and 8.
Thus, we have 4 options for arranging the numbers without considering the order of the numbers in the rows. Since the numbers in each row can be swapped, we get $2^{4}=16$ options for each arrangement. In total, we get 64 options. | 64 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1.1. Find all pairs of two-digit natural numbers for which the arithmetic mean is $25 / 24$ times greater than the geometric mean. In your answer, specify the largest of the arithmetic means for all such pairs. | Answer: 75.
Solution: Let $a, b$ be the required numbers (without loss of generality, we can assume that $a > b$) and let $\frac{a+b}{2}=25x$ and $\sqrt{ab}=24x$. Then $(\sqrt{a}+\sqrt{b})^2=a+b+2\sqrt{ab}=98x$ and $(\sqrt{a}-\sqrt{b})^2=$ $a+b-2\sqrt{ab}=2x$. From this, it follows that $\sqrt{a}+\sqrt{b}=7(\sqrt{a}-\sqrt{b})$. Therefore, $3\sqrt{a}=4\sqrt{b}$. Thus, $a:b=16:9$. Considering that $a$ and $b$ are two-digit numbers, the sum will be the largest for $a=16 \cdot 6=96, b=9 \cdot 6=54$. Their arithmetic mean is $\frac{96+54}{2}=75$. | 75 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2.1. The vertices of a cube are labeled with numbers $\pm 1$, and on its faces are numbers equal to the product of the numbers at the vertices of that face. Find all possible values that the sum of these 14 numbers can take. In your answer, specify their product. | Answer: -20160.
Solution. It is obvious that the maximum value of the sum is 14. Note that if we change the sign of one of the vertices, the sum of the numbers in the vertices will increase or decrease by 2. On the other hand, the signs of three faces will change. If their sum was $1, -1, 3, -3$, it will become $-1, 1, -3$, or 3, respectively, i.e., it will change by 2 or 6. It is clear that if we add two sums, the remainder when divided by 4 does not change. Therefore, we can obtain the numbers $10, 6, 2, -2$, $-6, -10$. The number -14, obviously, cannot be obtained, since this would require making all numbers equal to -1. For the other values, it is easy to construct corresponding examples. | -20160 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4.1. How many numbers from 1 to 1000 (inclusive) cannot be represented as the difference of two squares of integers? | Answer: 250.
Solution. Note that any odd number $2 n+1$ can be represented as $(n+1)^{2}-n^{2}$. Moreover, an even number that is a multiple of 4 can be represented as $4 n=(n+1)^{2}-(n-1)^{2}$. The numbers of the form $4 n+2$ remain. Note that a square can give remainders of 0 or 1 when divided by 4, so numbers of the form $4 n+2$ cannot be obtained as the difference of squares. There is exactly one such number (of the form $4 n+2$) in every set of four consecutive numbers, so the total number of such numbers from 1 to 1000 will be $1000 / 4=250$. | 250 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
6.1. On the coordinate plane, an isosceles right triangle with vertices at points with integer coordinates is depicted. It is known that there are exactly 2019 points with integer coordinates on the sides of the triangle (including the vertices). What is the smallest possible length of the hypotenuse of the triangle under these conditions? Provide the length of the hypotenuse, rounded to the nearest integer. | Answer: 952.
Solution. The smallest length of the hypotenuse corresponds to the case where the distance between the points is the smallest, which is only possible when the legs follow the grid lines (for a rotated triangle, the distance between the points will be no less than $\sqrt{2}$). Then each leg has a length of 673, and the hypotenuse is $673 \sqrt{2} \approx 952$. | 952 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
7.1. Natural numbers from 1 to some $n$ are written in a row. When one of the numbers was removed, it turned out that the arithmetic mean of the remaining numbers is $40 \frac{3}{4}$. Find the number that was removed. | Answer: 61.
Solution. The sum of numbers from 1 to $n$ is $S_{n}=\frac{n(n+1)}{2}$. Let the number removed be $m$, where $1 \leqslant m \leqslant n$. Then the condition of the problem can be written as
$$
\frac{S_{n}-m}{n-1}=40 \frac{3}{4}
$$
Transforming: $\frac{n+2}{2}-\frac{m-1}{n-1}=40 \frac{3}{4}$. Note that $\frac{m-1}{n-1} \leqslant 1$, so if $n$ is even, then $\frac{m-1}{n-1}=\frac{1}{4}$, and if odd, then $\frac{m-1}{n-1}=\frac{3}{4}$. In the first case, we get $n=80$, from which $m-1=79 \cdot \frac{1}{4}-$ not an integer. In the second case, $n=81$, i.e., $m-1=80 \cdot \frac{3}{4}=60$. | 61 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1.1. A ballpoint pen costs 10 rubles, a gel pen costs 50 rubles, and a fountain pen costs 80 rubles. What is the maximum number of gel pens that can be bought given that exactly 20 pens must be purchased in total, and among them there must be pens of all three types, and exactly 1000 rubles must be spent on them? | Answer: 13. Solution. If $x$ ballpoint pens, $y$ gel pens, and $z$ fountain pens are bought, then we have two equations: $x+y+z=20 ; 10 x+50 y+80 z=1000$ (or $x+5 y+8 z=100$ ). Subtracting the first equation from the second, we get $4 y+7 z=80$. It follows that $z$ must be divisible by 4, i.e., $z=4 n$. Therefore, $4 y+7 \cdot 4 n=80$, i.e., $y=20-7 n$. Accordingly, $x=20-y-z=3 n$. Positive solutions are obtained when $n=1$ and $n=2$. In the end, the solutions are two sets of integers: $(3,13,4)$ and $(6,6,8)$. The largest possible $y$ is 13. | 13 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4.1. Given the function $f(x)=|x+1|-2$. How many roots does the equation $f(f(\ldots f(f(x)) \ldots))=\frac{1}{2}$ have, where the function $f$ is applied 2013 times? | Answer: 4030. Solution. Considering the graph of the function $f$ (see Fig. 1), we conclude that $|f(x)+1|=f(x)+1$ and $|f(x)+1|-2=f(x)-1$. Therefore, the graph of the function $f(f(x))$
has the form as in $p and c$.
Fig. 1
Fig. 2
The equation $f(f(x))=\frac{1}{2}$ has 8 solutions. Note that between the rays $y=-x-4$, $x \leq-4$ and $y=x-3, x \geq 3$ there are exactly three triangles, the lengths of the bases of which are 2, and the heights are 1. The next substitution $f(f(f(x)))$ changes the graph of the function as follows: the rays $y=-x-4, x \leq-4$ and $y=x-3, x \geq 3$ will transition to the rays $y=-x-5, x \leq-5$ and $y=x-4, x \geq 4$, and another triangle will appear between them, the length of the base of which is 2, and the height is 1. Therefore, the equation $f(f(f(x)))=\frac{1}{2}$ has 10 solutions. Each subsequent substitution $f(\ldots)$ changes the graph of the function similarly: it shifts the extreme rays to the left and right by 1, respectively, and adds another triangle between the rays, the length of the base of which is 2, and the height is 1. Thus, starting from the function $f(f(x))$, each subsequent substitution $f(\ldots)$ increases the number of solutions of the previous equation by two. We get that if the function is applied 2013 times, then the number of roots of such an equation is $8+2 \cdot 2011=4030$. | 4030 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5.1. Specify the integer closest to the number $\sqrt{2012-\sqrt{2013 \cdot 2011}}+\sqrt{2010-\sqrt{2011 \cdot 2009}}+\ldots+\sqrt{2-\sqrt{3 \cdot 1}}$. | Answer: 31. Solution. The number given in the condition is equal to
$$
\frac{\sqrt{4024-2 \sqrt{2013 \cdot 2011}}+\sqrt{4010-2 \sqrt{2011 \cdot 2009}}+\ldots+\sqrt{4-2 \sqrt{3 \cdot 1}}}{\sqrt{2}}
$$
$=\frac{\sqrt{(\sqrt{2013}-\sqrt{2011})^{2}}+\sqrt{(\sqrt{2011}-\sqrt{2009})^{2}}+\ldots+\sqrt{(\sqrt{3}-\sqrt{1})^{2}}}{\sqrt{2}}$
$=\frac{\sqrt{2013}-\sqrt{2011}+\sqrt{2011}-\sqrt{2009}+\ldots+\sqrt{3}-\sqrt{1}}{\sqrt{2}}=\frac{\sqrt{2013}-1}{\sqrt{2}}$.
Since $\frac{\sqrt{2013}-1}{\sqrt{2}}=\frac{2012}{\sqrt{2013 \cdot 2}+\sqrt{2}}>\frac{2012}{64+1.5}=\frac{4024}{131}>30.7$, and
$\frac{\sqrt{2013}-1}{\sqrt{2}}=\frac{2012}{\sqrt{2013 \cdot 2}+\sqrt{2}}<\frac{2012}{63+1}=\frac{503}{16}<31.5$, the required integer is 31. | 31 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
8.1. Find the area of the figure defined on the coordinate plane by the inequality $2(2-x) \geq\left|y-x^{2}\right|+\left|y+x^{2}\right|$. | Answer: 15. Solution. In the region above the graphs of the functions $y=x^{2}$ and $y=-x^{2}$, the original inequality takes the form $2-x \geq y$. In the region below the graphs of the functions $y=x^{2}$ and $y=-x^{2}$, the original inequality takes the form $2-x \geq -y$, i.e., $y \geq x-2$. In the region lying above the graph of the function $y=-x^{2}$ and below the graph of the function $y=x^{2}$, the original inequality has the form $2-x \geq x^{2}$.
Therefore, the points $(x, y)$ satisfying the given inequality form a trapezoid $A B C D$ on the coordinate plane, bounded by the lines $y=-x+2$, $y=x-2, x=-2$ and $x=1$ (see figure), with vertices at the points $(-2 ;-4),(-2 ; 4),(1 ; 1)$ and $(1 ;-1)$.
Since $A B=8, C D=2$, and the height of the trapezoid is 3, the desired area is $\frac{8+2}{2} \cdot 3=15$ | 15 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
9.1. First-grader Masha, entering the school, each time climbs the school porch stairs, which have 10 steps. Being at the bottom of the stairs or on one of its steps, she can either go up to the next step or jump over one step up (Masha cannot yet jump over two or more steps). What is the minimum number of times Masha needs to enter the school to climb the porch in all possible ways? | Answer: 89. Solution. Note that Masha can climb a porch with one step in one way, and a porch with two steps in two ways: either stepping on each step, or, by stepping over the first step, landing directly on the second.
Let $a_{n}$ be the number of ways Masha can climb a porch with $n$ steps. Since Masha can reach the $n$-th step either from the $(n-1)$-th step or from the $(n-2)$-th step, then $a_{n}=a_{n-2}+a_{n-1}$.
We sequentially calculate: $a_{1}=1, a_{2}=2, a_{3}=1+2=3, a_{4}=2+3=5, a_{5}=3+5=8$, $a_{6}=5+8=13, a_{7}=8+13=21, a_{8}=13+21=34, a_{9}=21+34=55, a_{10}=34+55=89$.
Note that the numbers constructed according to the rule $F_{0}=0, F_{1}=1, F_{n}=F_{n-2}+F_{n-1}(n \geq 2)$ are called Fibonacci numbers. Thus, $a_{n}=F_{n+1}$. | 89 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
10.1. Having found some polynomial of the sixth degree $x^{6}+a_{1} x^{5}+\ldots+a_{5} x+a_{6}$ with integer coefficients, one of the roots of which is the number $\sqrt{2}+\sqrt[3]{5}$, write in the answer the sum of its coefficients $a_{1}+a_{2}+\ldots+a_{6}$. | Answer: -47. Solution. $x=\sqrt{2}+\sqrt[3]{5} \Rightarrow (x-\sqrt{2})^{3}=5 \Rightarrow x^{3}-3 x^{2} \sqrt{2}+3 x \cdot 2-2 \sqrt{2}=5$ $\Rightarrow x^{3}+6 x-5=(3 x^{2}+2) \cdot \sqrt{2} \Rightarrow (x^{3}+6 x-5)^{2}=(3 x^{2}+2)^{2} \cdot 2$ $\Rightarrow P_{6}(x)=(x^{3}+6 x-5)^{2}-2(3 x^{2}+2)^{2}$. In this case, the polynomial itself does not need to be explicitly obtained (for reference, note that this is the polynomial $x^{6}-6 x^{4}-10 x^{3}+12 x^{2}-60 x+17$), since we need the sum: $a_{1}+\ldots+a_{6}=P_{6}(1)-1=2^{2}-2 \cdot 5^{2}-1=-47$. | -47 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem 4. Each cell of a $3 \times 3$ table is painted in one of three colors such that cells sharing a side have different colors, and not all three colors need to be used. How many such colorings exist? | Answer: 246.
Solution. The central cell can be painted in any of the three colors, let's call this color $a$. Each of the four cells that share a side with the central one can be painted in any of the two remaining colors. Let the cell located above the central one be painted in color $b$. The third color we will call $c$. Consider all possible ways to paint the cells that share a side with the central one, and encode them with strings of letters $b$ and $c$, which start with the letter $b$, and then correspond to the colors of these cells, traversed counterclockwise. For example, the painting
| | $b$ | |
| :--- | :--- | :--- |
| $c$ | $a$ | $b$ |
| | $c$ | |
will be encoded by the string $b c c b$. Consider any corner cell. If the two cells that share a side with it are painted in the same color, then the corner cell can be painted in two ways. If these two cells are painted in different colors, then the corner cell can be painted in only one way. We will construct a table in which, for each of the 8 obtained encoding strings, we will indicate the number of ways to paint the corner cells.
| $b b b b$ | 16 | $b b c b$ | 4 | $b c b b$ | 4 | $b c c b$ | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $b b b c$ | 4 | $b b c c$ | 4 | $b c b c$ | 1 | $b c c c$ | 4 |
Thus, the desired number of colorings is the product of the number of ways to paint the central cell, the number of ways to paint the cell located above the central one, and the sum of the numbers in the constructed table: $3 \cdot 2 \cdot(16+6 \cdot 4+1)=246$. | 246 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
2.1. Once, in a company, the following conversation took place:
- We must call Misha immediately! - exclaimed Vanya.
However, no one remembered Misha's phone number.
- I remember for sure that the last three digits of the phone number are consecutive natural numbers, - said Nastya.
- And I recall that the first five digits formed a palindrome, - noted Anton.
- Seven-digit numbers are not memorized as a whole; they are broken down into three groups: first three digits, and then two groups of two digits each. I think the three-digit number obtained in this way was divisible by 9 - remarked Nikita.
- That's right, - supported Mitya, - and there were three consecutive ones in the phone number.
- Only one of the two-digit numbers obtained by Nikita's method was prime, - added Sasha.
Help the guys restore Misha's phone number. | Answer: 7111765.
Solution. Note that three consecutive ones cannot stand at the beginning, as 111 is not divisible by 9. Therefore, among the first three digits, there is one that is different from one. If this is the second or third digit, then since the first five form a palindrome and the last three are consecutive natural numbers, there will be no three consecutive ones in the number. Therefore, the second, third, and fourth digits are ones, then the first and fifth are sevens. This means that the first two-digit number in the Nikitin division is 17 (a prime number). The last three digits will be consecutive natural numbers if the second two-digit number is 89 or 65. But since 89 is a prime number, the only option left is 65. Therefore, the desired number is 7111765. | 7111765 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4.1. We will call a natural number interesting if all its digits, except the first and last, are less than the arithmetic mean of the two adjacent digits. Find the largest interesting number. | Answer: 96433469.
Solution. Let $a_{n}$ be the n-th digit of the desired number. By the condition, $a_{n}9$. Similarly, there cannot be four negative differences. Therefore, the maximum number of such differences can be 7, and the desired number is an eight-digit number. To make it the largest, the first digit should be 9, and the first differences between the digits should be as small as possible. If the differences are sequentially $3,2,1,0,-1,-2,-3$, then we get the answer: 96433469. | 96433469 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5.1. Find the smallest natural solution of the inequality $2^{x}+2^{x+1}+\ldots+2^{x+2000}>2^{2017}$. Answer. 17. | Solution. The value $x=17$ is clearly a solution. If $x \leqslant 16$, then we have
$$
2^{x}+2^{x+1}+\ldots+2^{x+2000} \leqslant 2^{16}+2^{17}+\ldots+2^{2015}+2^{2016}<2^{2017}
$$
since this inequality reduces sequentially to the following: $2^{16}+2^{17}+\ldots+2^{2015}<$ $2^{2017}-2^{2016}=2^{2016}, 2^{16}+2^{17}+\ldots+2^{2014}<2^{2016}-2^{2015}=2^{2015}, \ldots, 2^{16}+2^{17}<2^{19}-2^{18}=2^{18}$, $2^{16}<2^{18}-2^{17}=2^{17}$, which is true. | 17 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
6.1. How many triangles with integer sides have a perimeter equal to 27? (Triangles that differ only in the order of the sides - for example, $7,10,10$ and $10,10,7$ - are considered the same triangle.) | Answer: 19.
Solution: Arrange the sides in ascending order: $a \leqslant b \leqslant c$. Then the smaller side $a$ does not exceed 9. If $a=1$ or $a=2$, there is one such triangle. If $a=3$ or $a=4$, there are two such triangles. If $a=5$ or $a=6$, there are three such triangles. If $a=7$, there are four such triangles. If $a=8$, there are two such triangles. If $a=9$, there is one such triangle. In total, we get 19 triangles. | 19 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
2. First-grader Petya was laying out a contour of an equilateral triangle with the chips he had, so that each of its sides, including the vertices, contained the same number of chips. Then, with the same chips, he managed to lay out the contour of a square in the same way. How many chips does Petya have, if each side of the square contains 2 chips less than each side of the triangle? | Answer: 24.
Solution. Let the side of the triangle contain $x$ chips, and the side of the square - $y$ chips. The total number of chips, counted in two ways, is $3 x-3=4 y-4$ (we account for the corner chips being counted twice). From the problem statement, it follows that $y=x-2$. Therefore, we get the equation $3(x-1)=4(x-3)$, from which $x=9$. Thus, the total number of chips is $3 \cdot 9-3=24$. | 24 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
8. In how many different ways can integers $a, b, c \in [1,100]$ be chosen so that the points with coordinates $A(-1, a), B(0, b)$, and $C(1, c)$ form a right triangle? | Answer: 974
Solution: $A B^{2}=1+(b-a)^{2}, B C^{2}=1+(c-b)^{2}, A C^{2}=4+(c-a)^{2}$.
If triangle $A B C$ is a right triangle with hypotenuse $A C$, then by the Pythagorean theorem $A C^{2}=A B^{2}+B C^{2}, 1+(b-a)^{2}+1+(b-c)^{2}=4+(a-c)^{2}$, which simplifies to $(b-a)(b-c)=1$. Since both factors are integers, we have only the following cases: $b=a+1=c+1$ and $b=a-1=c-1$, for each of which there are 99 triples $(a, b, c)$, i.e., 198 ways.
If the hypotenuse is side $A B$, then similarly we get the relation $(c-a)(c-b)=-2$, which is possible only in the following cases:
$c=a+1=b-2$
$c=a-1=b+2$
$c=a+2=b-1$
$c=a-2=b+1$
for each of which there are 97 triples $(a, b, c)$, i.e., a total of $97 \cdot 4=388$ ways.
If the hypotenuse is side $B C$, then we get the relation $(a-b)(a-c)=-2$. Similarly, we find 388 ways.
In total, we get $198+388+388=974$ ways. | 974 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1. Nезнayka jumped from his house to Znayka's house. For the first three-quarters of the path, he jumped with jumps the length of two of his usual steps, and for the remaining quarter of the path, he jumped with jumps the length of three of his usual steps. It turned out that the number of jumps of two steps was 350 more than the number of jumps of three steps. How many usual steps is it from Znayka's house to Nезнayka's house? Assume that all steps of Nезнayka are the same.
Solution. Let the desired distance be $S$ steps, then the number of jumps of two and three steps is $\frac{3 S}{4 \cdot 2}$ and $\frac{S}{4 \cdot 3}$, respectively. We obtain the relationship $\frac{3 S}{8}-\frac{S}{12}=350 \Leftrightarrow \frac{7 S}{24}=350 \varnothing$ $S=1200$ (steps). | Answer variant l: 1200.
Answer variant 2: 1800.
Answer variant $3: 2040$.
Answer variant 4: 900.
Scoring evaluation: 15 баллов - correct solution and correct answer; 10 баллов - arithmetic error in otherwise correct solution | 1200 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
8. What is the least number of odd numbers that can be chosen from the set of all odd numbers lying between 16 and 2016, so that no one of the chosen numbers is divisible by any other?
| Solution. We will select all odd numbers from 673 to 2015, their quantity is
$\frac{2015-671}{2}=672$. None of these numbers is divisible by another, because in division, the result should be an odd number, which is at least 3, but $673-3>2015$.
We will show that it is impossible to select more than 672 numbers satisfying the condition of the problem. Indeed, let's divide all odd numbers from 17 to 2015 into 672 groups, generated by the selected numbers and including the generating number and all its divisors, such that the result of division by which is a power of three: $\{2015\},\{2013,671\},\{2011\},\{2009\},\{2007,669,223\}, \ldots,\{675,225, 75,25\},\{673\}$. If more than 672 numbers are selected, then by the pigeonhole principle, at least two of them will end up in the same group, meaning one of them will be divisible by the other.
Note that the selected set of 672 numbers is not unique. For example, if we replace the number $2013=671 \cdot 3$ with 671, the new set will also satisfy the condition of the problem.
Answer variant 1: 672. Suitable, for example, the set 673,..., 2015.
Answer variant 2: 667. Suitable, for example, the set 669, ..., 1999.
Answer variant 3: 673. Suitable, for example, the set 673, ..., 2017.
Answer variant 4: 670. Suitable, for example, the set 671, ..., 2009.
Scoring criteria: 15 points - correct reasoning and correct answer, 10 points - correct answer and a correct example provided, but no proof that more numbers cannot be selected.
## 2015/2016 academic year CRITERIA FOR DETERMINING WINNERS AND PRIZE WINNERS ${ }^{1}$ of the schoolchildren's olympiad «LOMONOSOV» in mathematics 10-11 grades ELIMINATION STAGE
WINNER:
From 91 points inclusive and above.
PRIZE WINNER:
From 60 points to 90 points inclusive.
## FINAL STAGE
WINNER (Diploma I degree):
From 90 points inclusive and above.
PRIZE WINNER (Diploma II degree):
From 80 points to 89 points inclusive.
PRIZE WINNER (Diploma III degree):
From 65 points to 79 points inclusive.[^0]
[^0]: ${ }^{1}$ Approved at the meeting of the jury of the schoolchildren's olympiad «Lomonosov» in mathematics | 672 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1.1. (4 points) Find the least common multiple of the numbers 28 and 72. | Answer: 504.
Solution. We have $28=2^{2} \cdot 7, 72=2^{3} \cdot 3^{2}$, therefore $\operatorname{LCM}(28,72)=2^{3} \cdot 3^{2} \cdot 7=504$. | 504 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1.4. Find the greatest common divisor of the numbers 144 and 120. | Answer: 24.
Solution. We have $144=2^{4} \cdot 3^{2}, 120=2^{3} \cdot 3 \cdot 5$, so $\text{GCD}(144,120)=2^{3} \cdot 3=24$. | 24 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
2.1. (16 points) A team consisting of juniors and masters from the "Vimpel" sports society went to a shooting tournament. The average number of points scored by the juniors turned out to be 22, by the masters - 47, and the average number of points for the entire team - 41. What is the proportion (in percent) of masters in this team | Answer: 76.
Solution. Let there be $x$ juniors and $y$ masters in the team. Then the total number of points scored by the team is $22x + 47y = 41(x + y)$, from which we find $19x = 6y$. Therefore, the proportion of masters is $\frac{y}{x+y} = \frac{19y}{19x + 19y} = \frac{19y}{25y} = 0.76$, i.e., $76\%$. | 76 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3.1. (16 points) A square with a side of 36 cm was cut into three rectangles such that the areas of all three rectangles are equal and any two rectangles share a common boundary segment. What is the total length (in cm) of the cuts made? | Answer: 60.
Solution. One cut has a length of 36 cm and separates one of the rectangles (see fig.). The remaining 2 rectangles have a common side $x$, so they are both $18 \times x$ cm in size. Therefore,

$18 \cdot x=36^{2} / 3$, from which $x=24$ cm. Thus, the total length of the cuts is 60 cm. | 60 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4.1. (16 points) An eraser, 3 pens, and 2 markers cost 240 rubles, while 2 erasers, 4 markers, and 5 pens cost 440 rubles. What is the total cost (in rubles) of 3 erasers, 4 pens, and 6 markers? | Answer: 520.
Solution. From the condition, it follows that 3 erasers, 8 pens, and 6 markers cost $440+240=680$ rubles. Moreover, 2 erasers, 6 pens, and 4 markers will cost $2 \cdot 240=480$ rubles. Therefore, one pen costs $480-440=40$ rubles. Then, 3 erasers, 4 pens, and 6 markers cost $680-4 \cdot 40=520$ rubles. | 520 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5.1. (16 points) A squirrel jumps once a minute to a distance of 1 along the number line, starting from point 0, and in any direction. She jumped for 40 minutes, after which she fell asleep. How many points on the number line could the squirrel have fallen asleep in? | Answer: 41.
Solution. We will solve the problem in a general form. Let the squirrel have jumped for $N$ minutes. If $N$ is even $(N=2 n)$, then after $2 n$ steps, the squirrel can only reach a point with an even coordinate in the range from $-2 n$ to $2 n$, and it can reach any of these points (to a point with coordinate $2 k$, it can jump in $2 k$ of the first minutes, and change direction each subsequent minute). From $-2 n$ to $2 n$, there are $2 n+1=N+1$ such points.
If the number of minutes is odd ( $N=2 n+1$ ), then after $2 n+1$ steps, the squirrel can only reach a point with an odd coordinate in the range from $-2 n-1$ to $2 n+1$, and it can reach any of these points (to a point with coordinate $2 k+1$, it can jump in $2 k+1$ of the first minutes, and change direction each subsequent minute). From $-2 n-1$ to $2 n+1$, there are $2 n+2=N+1$ such points. | 41 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6.1. (16 points) In a hut, several inhabitants of the island gathered, some from the Ah tribe, and the rest from the Ukh tribe. The inhabitants of the Ah tribe always tell the truth, while the inhabitants of the Ukh tribe always lie. One of the inhabitants said: "There are no more than 16 of us in the hut," and then added: "We are all from the Ukh tribe." Another said: "There are no more than 17 of us in the hut," and then noted: "Some of us are from the Ah tribe." The third said: "There are five of us in the hut," and, looking around, added: "There are no fewer than three inhabitants of the Ukh tribe among us." How many inhabitants of the Ah tribe are in the hut? | Answer: 15.
Solution. A resident of tribe Ah cannot say "we are all from tribe Ukh," so the first one is from tribe Ukh. Therefore, there are no fewer than 17 people in the hut. So the second one spoke the truth, i.e., he is from tribe Ah. Therefore, there are no more than 17 people in the hut. Thus, there are 17 people in the hut. The third one is from tribe Ukh, as he said there are five of them in total. But since he said there are no fewer than three residents from tribe Ukh, there are no more than two. Two have already been found (the third and the first), so there are exactly two. Then the number of residents from tribe Ah is 15. | 15 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
1.1. Once, in a company, the following conversation took place:
- We must call Misha immediately! - exclaimed Vanya.
However, no one remembered Misha's phone number.
- I remember for sure that the last three digits of the phone number are consecutive natural numbers, - said Nastya.
- And I recall that the first five digits formed a palindrome, - noted Anton.
- Seven-digit numbers are not memorized as a whole; they are broken down into three groups: first three digits, and then two groups of two digits each. I think the three-digit number obtained in this way was divisible by 9 - remarked Nikita.
- That's right, - supported Mitya, - and there were three consecutive ones in the phone number.
- Only one of the two-digit numbers obtained by Nikita's method was prime, - added Sasha.
Help the guys restore Misha's phone number. | Answer: 7111765.
Solution. Note that three consecutive ones cannot stand at the beginning, as 111 is not divisible by 9. Therefore, among the first three digits, there is one that is different from one. If this is the second or third digit, then since the first five form a palindrome and the last three are consecutive natural numbers, there will be no three consecutive ones in the number. Therefore, the second, third, and fourth digits are ones, then the first and fifth are sevens. This means that the first two-digit number in the Nikitin partition is 17 (a prime number). The last three digits will be consecutive natural numbers if the second two-digit number is 89 or 65. But since 89 is a prime number, the only option left is 65. Therefore, the desired number is 7111765. | 7111765 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
3.1. Find the largest integer solution of the inequality $2^{x}+2^{x+1}+\ldots+2^{x+2000}<1$. | Answer: -2001.
Solution. By factoring out $2^{x}$ and using the formula for the sum of the first terms of a geometric progression, we can transform the inequality to $2^{x} \cdot\left(2^{2001}-1\right)<1$. For $x \geqslant-2000$, this inequality is not satisfied. If, however, $x=-2001$, we get $1-2^{-2001}<1$, which is true. | -2001 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
5.1. How many triangles with integer sides have a perimeter equal to 2017? (Triangles that differ only in the order of their sides, for example, 17, 1000, 1000 and 1000, 1000, 17, are counted as one triangle.) | Answer: 85008.
Solution. Let the sides of the triangle be $a, b, c$ ordered such that $a \leqslant b \leqslant c$. Then the smaller side $a$ does not exceed $2017 / 3=672 \frac{1}{3}$.
Consider the case of even $a$, i.e., $a=2 k$. Then for $k=1, \ldots, 252$, there will be $k$ triangles each, totaling $253 \cdot 252 / 2=31878$ triangles. For $k=253, \ldots, 336$, there will be $1009-3 k$ triangles each, totaling $1009 \cdot(336-253+1)-3 \cdot(336 \cdot 337 / 2-252 \cdot 253 / 2)=10542$ triangles.
Similarly, for odd $a, a=2 k-1$, for $k=1, \ldots, 252$, there will be $k$ triangles each, totaling $253 \cdot 252 / 2=31878$ triangles. For $k=253, \ldots, 336$, there will be $1011-3 k$ triangles each, totaling $1011 \cdot(336-253+1)-3 \cdot(336 \cdot 337 / 2-252 \cdot 253 / 2)=10710$ triangles.
In total, we get $31878+10542+31878+10710=85008$ triangles. | 85008 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 1. Three friends, weightlifters A, B, and C, came to a competition. They all competed in the same weight category, and one of them became the winner. If the weight lifted by weightlifter A is added to the weight lifted by weightlifter B, the total is 220 kg. If the weights lifted by weightlifters A and C are added together, the total is 240 kg, and if the weights lifted by weightlifters B and C are added together, the total is 250 kg. What weight did the winner of the competition lift? | Answer: 135.
Solution. The sum of three weights is $(220+240+250) / 2=355$. Therefore, V lifted $355-220=135$, B lifted $355-240=115$, A lifted $355-250=105$. The winner is $\mathrm{B}=135$. | 135 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. How many solutions in integers does the equation
$$
\frac{1}{2022}=\frac{1}{x}+\frac{1}{y} ?
$$ | Answer: 53.
Solution. By eliminating the denominators, we obtain the equation
\[
(x-2022)(y-2022)=2022^{2}.
\]
Since \(2022^{2}=2^{2} \cdot 3^{2} \cdot 337^{2}\), the number \(x-2022\) can have the factors \(2^{0}, 2^{1}, 2^{2}\) - a total of three options. Similarly for the other factors. The number \(x-2022\) thus has \(3 \cdot 3 \cdot 3=27\) possible natural values, which means 54 integer values. However, one of these corresponds to \(x=0\), which does not satisfy the original equation. Therefore, there are 53 roots (for each suitable value of \(x\), we have \(y=\frac{2022^{2}}{x-2022}+2022\) - an integer). | 53 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 5. From the digits $a, b, c, d, e$, a five-digit number $\overline{a b c d e}$ is formed. For the two-digit numbers $\overline{a b}, \overline{b c}, \overline{c d}, \overline{d e}$, formed from the same digits, it is known that
$$
(\overline{a b}+\overline{b c})(\overline{b c}+\overline{c d})(\overline{c d}+\overline{d e})=157605
$$
Find the number $\overline{a b c d e}$. Multi-digit numbers cannot start with zero. | Answer: 12345 or 21436.
Solution. Note that $157605=3 \cdot 5 \cdot 7 \cdot 19 \cdot 79$. To start, we need to understand which combinations of prime factors correspond to the sums of two-digit numbers. The sum of two-digit numbers cannot exceed $99+99=198$, and $79 \cdot 3$ is already greater than 200, so one of the brackets must be 79. How can the remaining factors be distributed? 79(19.5)(3.7); 79(19.7)(3.5); 79(3.19)(5.7); $79(19)(3 \cdot 5 \cdot 7)$. There are no other cases because in them, a factor greater than 198 is obtained.
Thus, we get the triplets of numbers $(79 ; 95 ; 21),(79 ; 133 ; 15),(79 ; 57 ; 35),(79 ; 19 ; 105)$. Now, note the following: $(\overline{x y}+\overline{y z})=10 x+y+10 y+z=10(x+y)+(y+z)$, and the sums of the digits cannot exceed $9+9=18$. For example, if $(\overline{x y}+\overline{y z})=79$, then this means that $x+y=7$, $y+z=9$. If $(\overline{x y}+\overline{y z})=133$, then either $x+y=13, y+z=3$, or $x+y=12, y+z=13$. If $(\overline{x y}+\overline{y z})=15$, then either $x+y=1, y+z=5$, or $x+y=0, y+z=15$. For instance, we will focus on the set of numbers $(7,9),(12,13),(1,5)$, where the numbers represent possible sums of adjacent digits $\overline{a b c d e}$.
However, if we take the number $\overline{a b c d e}$, it will have only 4 possible pairs of adjacent digits, so the set can have no more than 4 different values. Thus, we rule out the chosen set, as well as all others except one, which will be ( $79 ; 57 ; 35$ ), with the numbers $(7,9),(5,7),(3,5)$. It has only 4 different values: $9,7,5,3$. Moreover, these pairs of numbers need to be arranged so that the values "fit together," that is, like this: $(3,5),(5,7),(7,9)$. Therefore, for $\overline{a b c d e}$, the following will be true: $a+b=3, b+c=5, c+d=7, d+e=9$. This system has only 4 solutions, corresponding to the 5-digit sequences $12345,21436,30527,03254$, the last of which is not suitable because it starts with zero, and the second to last - because for this sequence $\overline{b c}=05$. | 12345 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Task 1. Find the smallest natural number that has the following property: the remainder of its division by 20 is one less than the remainder of its division by 21, and the remainder of its division by 22 is 2. | Answer: 838.
Solution. The desired number is $20k + a = 21l + a + 1 = 22m + 2$, where $0 \leqslant a \leqslant 19$ and $l, k, m \geqslant 0$. From the first equation and the congruence modulo 20, we get that $l + 1 \equiv 0 \pmod{20}$. Since we are looking for the smallest number, let's try $l = 19$, if this $l$ does not work, then consider $l = 19 + 20 = 39$, and so on. We seek the desired number in the form $21 \cdot 19 + a + 1 = 22m + 2$, compare modulo 22: $3 + a + 1 \equiv 2 \pmod{22}$, hence, $a \equiv 20 \pmod{22}$, which is impossible. Now we seek the desired number in the form $21 \cdot 39 + a + 1 = 22m + 2$, so $5 + a + 1 \equiv 2 \pmod{22}$, that is, $a \equiv 18 \pmod{22}$. The number $21 \cdot 39 + 18 + 1 = 838$ satisfies the condition and is the smallest by construction. | 838 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. Find the three last digits of the number $10^{2022}-9^{2022}$. | Answer: 119.
Solution. Since $A=10^{2022}-(10-1)^{2022}=10^{2022}-10^{2022}+2022 \cdot 10^{2021}-C_{2022}^{2} \cdot 10^{2022}+\ldots+$ $C_{2022}^{3} \cdot 10^{3}-C_{2022}^{2} \cdot 10^{2}+C_{2022}^{1} \cdot 10-1$, then $A(\bmod 1000) \equiv-C_{2022}^{2} \cdot 100+C_{2022}^{1} \cdot 10-1(\bmod 1000) \equiv$ $-\frac{2022 \cdot 2021 \cdot 100}{2}+20220-1(\bmod 1000) \equiv-100+220-1 \equiv 119$. | 119 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 7. There is a certain number of identical plastic bags that can be nested inside each other. If all the other bags end up inside one of the bags, we will call this situation a "bag of bags." Calculate the number of ways to form a "bag of bags" from 10 bags.
## Explanation. Denote a bag with parentheses.
If there was one bag, there is only one way to form a "bag of bags": (). Two bags can also be formed in only one way: (()).
Three bags can be formed in two different ways: (()()) and ((())), and so on.
The order of the bags inside a bag does not matter. For example, the variant $((())())$ is not different from $(()(()))$. | Solution. If $\Pi_{n}$ denotes the number of ways for $n$ packages, then:
$$
\begin{gathered}
\Pi_{1}=1, \Pi_{2}=1, \Pi_{3}=2, \Pi_{4}=4, \Pi_{5}=9, \Pi_{6}=20, \Pi_{7}=48, \Pi_{8}=115, \Pi_{9}=286 \\
\Pi_{10}=719
\end{gathered}
$$
The problem is solved by enumerating the cases. For example, if we take $\Pi_{5}$:
$\Pi_{5}=P_{4}+P_{3}+P_{2}+P_{1}$, where $P_{k}$ is the number of ways corresponding to the case when the root package contains $k$ packages.
$P_{4}=1$, there is only one way: $(()()()()$.
$P_{3}=1$, there is also only one way: $((())()())$.
$P_{2}=3$, there are three ways to split 4 packages into 2 groups: 3 and 1, 2 and 2. The first way corresponds to $\left(\Pi_{3}()\right)$ - two variants, the second way - one variant, $((())(()))$.
$P_{4}=\Pi_{4}$ ways: $\left(\Pi_{4}\right)$.
In total, it is $1+1+(2+1)+4=9$.
As $n$ grows, cases will arise where one must be careful with combinatorics. For example, 8 packages can be arranged as $\left(\Pi_{3} \Pi_{3} \Pi_{1}\right)$, or as $\left(\Pi_{3} \Pi_{2} \Pi_{2}\right)$. In the second case, this is $\Pi_{3} \cdot \Pi_{2} \cdot \Pi_{2}=2 \cdot 1 \cdot 1=2$ ways, while in the first case - not $\Pi_{3} \cdot \Pi_{3} \cdot \Pi_{1}=2 \cdot 2 \cdot 1=4$, but actually only three, because the order of the triple packages does not matter. | 719 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. Find a two-digit number, the digits of which are different and the square of which is equal to the cube of the sum of its digits. | Answer: 27.
Solution: Let's write the condition as $\overline{A B}^{2}=(A+B)^{3}$. Note that the sum of the digits ( $A+B$ ) does not exceed 17, i.e., $\overline{A B}^{2} \leq 17^{3}$. Moreover, this number $\overline{A B}^{2}=n^{6}$, where $n-$
is some natural number that does not exceed 4. However, 1 and 2 do not work, since their cubes are single-digit numbers. Only 3 and 4 remain, and direct verification shows that $27^{2}=(2+7)^{2}=729$. | 27 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. On a circle, 25 points are marked, painted either red or blue. Some of the points are connected by segments, with one end of each segment being blue and the other end red. It is known that there do not exist two red points that belong to the same number of segments. What is the maximum possible number of red points? | Answer: 13.
Solution: Let's take 13 red and 12 blue points. The first red point is not connected to any other, the second is connected to one blue, ..., the 13th is connected to 12 blue points. Obviously, there cannot be more red points, because if there are more than 13, the number of connection options is less than 13, i.e., (by the pigeonhole principle) some two red points will belong to the same number of segments. | 13 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
7. Given the polynomial $P(x)=x^{5}+a_{4} x^{4}+a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0}$, it is known that $P(2014)=1, P(2015)=2, P(2016)=3, P(2017)=4$, $P(2018)=5$. Find $P(2013)$. | Answer: $-5!=-120$. Solution. Consider the polynomial $P(x)-x+2013$, the numbers $2014, \ldots 2018$ are its roots. Therefore (since the leading coefficient is 1) it can be represented as $P(x)-x+2013=$ $(x-2014)(x-2015) \cdot \ldots \cdot(x-2018)$. Substituting $x=2013$, we get $P(2013)-2013+2013=-120$. | -120 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. A flea jumps along the number line, and the length of each jump cannot be less than $n$. It starts its movement from the origin and wants to visit all integer points belonging to the segment $[0,2013]$ (and only them!) exactly once. For what greatest value of $n$ will it be able to do this? | Answer: $n=1006$.
Solution: For $n=1006$, a path can be constructed as follows:
$$
0 \rightarrow 1007 \rightarrow 1 \rightarrow 1008 \rightarrow \ldots \rightarrow 1005 \rightarrow 2012 \rightarrow 1006 \rightarrow 2013
$$
We will prove that $n$ cannot be greater than 1006. Indeed, suppose $n \geqslant 1007$. Then the point with coordinate 1007 can only be reached from the start of the segment (point 0). However, if the flea jumps from there to point 1007, it cannot jump back, so it must end its path at this point and will not visit other points on the segment. | 1006 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. Find the number of 9-digit numbers in which each digit from 1 to 9 appears exactly once, the digits 1, 2, 3, 4, 5 are arranged in ascending order, and the digit 6 appears before the digit 1 (for example, 916238457). | Answer: 504
Solution: Note that after arranging the digits $7,8,9$, the remaining digits are uniquely determined. Therefore, the number of such numbers is $7 \cdot 8 \cdot 9=504$. | 504 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1.1. From the digits 1, 3, and 5, different three-digit numbers are formed, each of which has all distinct digits. Find the sum of all such three-digit numbers. | Answer: 1998 (all possible numbers: $135,153,315,351,513,531$ ). | 1998 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1.2. From the digits 1, 2, and 5, different three-digit numbers are formed, each of which has all distinct digits. Find the sum of all such three-digit numbers. | Answer: 1776 (all possible numbers: 125, 152, 215, 251, 512, 521). | 1776 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
3.1. The decreasing sequence $a, b, c$ is a geometric progression, and the sequence $577 a, \frac{2020 b}{7}, \frac{c}{7}$ is an arithmetic progression. Find the common ratio of the geometric progression. | Answer: 4039.
Solution. Let $b=a q, c=a q^{2}$. The properties of an arithmetic progression and the conditions of the problem lead to the equation $2 \cdot \frac{2020 a q}{7}=577 a+\frac{a q^{2}}{7} \Leftrightarrow q^{2}-4040 q+4039=0$, from which $q=1$ or $q=4039$. A decreasing geometric progression can only occur when $q=4039$ (for example, if $a=-1$). | 4039 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
7.1. The numbers $p$ and $q$ are chosen such that the parabola $y=p x-x^{2}$ intersects the hyperbola $x y=q$ at three distinct points $A, B$, and $C$, and the sum of the squares of the sides of triangle $A B C$ is 324, while the centroid of the triangle is 2 units away from the origin. Find the product $p q$. | Answer: 42.
Solution. The system $y=p x-x^{2}, x y=q$ reduces to the cubic equation $x^{3}-p x^{2}+q=0$, which has, according to the problem, three distinct roots $x_{1}, x_{2}, x_{3}$, since the abscissas of any two different points on the curve $y=p x-x^{2}$ are distinct. By Vieta's theorem,
$$
x_{1}+x_{2}+x_{3}=p, \quad x_{1} x_{2}+x_{1} x_{3}+x_{2} x_{3}=0, \quad x_{1} x_{2} x_{3}=-q .
$$
Let $A\left(x_{1}, y_{1}\right), B\left(x_{2}, y_{2}\right), C\left(x_{3}, y_{3}\right)$. Note that if at least one of the numbers $x_{1}, x_{2}$, or $x_{3}$ is 0, then $q=0$, and the cubic equation will have only two roots, which contradicts the problem's condition. Then, from the system,
$$
y_{1}=\frac{q}{x_{1}}, \quad y_{2}=\frac{q}{x_{2}}, \quad y_{3}=\frac{q}{x_{3}}
$$
from which
$$
y_{1}+y_{2}+y_{3}=q \frac{x_{1} x_{2}+x_{1} x_{3}+x_{2} x_{3}}{x_{1} x_{2} x_{3}}=0 ; \quad y_{1} y_{2}+y_{2} y_{3}+y_{1} y_{3}=q^{2} \frac{x_{1}+x_{2}+x_{3}}{x_{1} x_{2} x_{3}}=-p q
$$
The point $M$ of intersection of the medians of triangle $A B C$ has coordinates
$$
\left(\frac{1}{3}\left(x_{1}+x_{2}+x_{3}\right), \frac{1}{3}\left(y_{1}+y_{2}+y_{3}\right)\right)
$$
Taking into account Vieta's theorem, we have $M\left(\frac{p}{3}, 0\right)$. Now we will calculate the sum of the squares of the lengths of the sides of triangle $A B C$. It is equal to
$$
\begin{gathered}
\left(x_{1}-x_{2}\right)^{2}+\left(x_{2}-x_{3}\right)^{2}+\left(x_{3}-x_{1}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(y_{2}-y_{3}\right)^{2}+\left(y_{3}-y_{1}\right)^{2}= \\
=2\left(x_{1}+x_{2}+x_{3}\right)^{2}-6\left(x_{1} x_{2}+x_{2} x_{3}+x_{1} x_{3}\right)+2\left(y_{1}+y_{2}+y_{3}\right)^{2}-6\left(y_{1} y_{2}+y_{2} y_{3}+y_{1} y_{3}\right)=2 p^{2}+6 p q
\end{gathered}
$$
According to the problem's condition, $\left|\frac{p}{3}\right|=2,2 p^{2}+6 p q=324$, from which we find two pairs: $(p ; q)=(6 ; 7)$ or $(p ; q)=(-6 ;-7)$. In both cases, $p q=42$. | 42 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
9.1. How many natural numbers $n \in [20182019 ; 20192018]$ are there for which the number $\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}\right]$ is even? (Here, $[x]$ denotes the greatest integer not exceeding $x$.) | Answer: 4999.
Solution. Consider the sequences
$$
x_{n}=\left(\frac{1+\sqrt{5}}{2}\right)^{n}, \quad y_{n}=\left(\frac{1-\sqrt{5}}{2}\right)^{n}, \quad a_{n}=x_{n}+y_{n}
$$
Since $-1<\frac{1-\sqrt{5}}{2}<0$, we have $y_{n} \in(0 ; 1)$ for even $n$, and $y_{n} \in(-1 ; 0)$ for odd $n$. Then $\left[x_{n}\right]=\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}\right]$ for even $n$ equals $a_{n}-1$, and for odd $n$ it is simply $a_{n}$. Moreover, we have $a_{n+2}=a_{n+1}+a_{n}$ for all natural $n$. Since $a_{1}=1, a_{2}=3$, then $a_{3}=4$ and we get such a parity sequence for $a_{n}(n=1,2, \ldots)$: odd, odd, even, odd, odd, even, $\ldots$
Then $\left[x_{n}\right]$ is related to $a_{n}$ as follows:
| $n$ | $6 k$ | $6 k+1$ | $6 k+2$ | $6 k+3$ | $6 k+4$ | $6 k+5$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $a_{n}$ | even | odd | odd | even | odd | odd |
| $\left[x_{n}\right]$ | $a_{n}-1$ | $a_{n}$ | $a_{n}-1$ | $a_{n}$ | $a_{n}-1$ | $a_{n}$ |
| $\left[x_{n}\right]$ | odd | odd | even | even | even | odd |
Since $x_{n}=a_{n}-y_{n}$, for numbers $n$ of the form $6 k, 6 k+1, 6 k+5$, the number $\left[x_{n}\right]$ is odd, and for numbers $n$ of the form $6 k+2, 6 k+3, 6 k+4$ it is even. Since $20182019=6 k_{1}+5, 20192018=6 k_{2}+2$, among the numbers $n=20182019, \ldots, 20192018$ the desired number is $3 \cdot \frac{20192018-20182022}{6}+1=4999$. | 4999 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
6. Pete was given a new electric jigsaw on his birthday, with a feature to count the length of the cuts made. To try out the gift, Pete took a square piece of plywood with a side of 50 cm and cut it into squares with sides of 10 cm and 20 cm. How many squares in total were obtained, if the electric jigsaw shows a total cut length of $2 \mathbf{m} 80 \mathrm{~cm}$? | Answer: 16. Solution. The perimeter of the figures must be taken into account, in addition to the perimeter of the original square, from which we get that the total perimeter of the resulting squares is $280 \cdot 2 + 200 = 760$. Now, we can denote the number of squares through $x$ and $y$ respectively and solve the system $\left\{\begin{array}{c}10^{2} \cdot x + 20^{2} \cdot y = 50^{2}, \\ 4 \cdot 10 \cdot x + 4 \cdot 20 \cdot y = 760,\end{array}\right.$ or proceed with the following reasoning. If all the squares had a side of 10, there would be $6 \mathbf{~} 25$ of them, then the total perimeter would be $25 \cdot 40 = 1000$. If we replace four small squares $10 \times 10$ with one square $20 \times 20$, the perimeter would decrease by $160 - 80 = 80$ cm. To get 760 from 1000, this needs to be done 3 times. Therefore, there will be 3 squares $20 \times 20$ and 13 squares $10 \times 10$—a total of 16 squares.
## 2015/2016 Academic Year CRITERIA FOR DETERMINING WINNERS AND PRIZE WINNERS ${ }^{2}$ of the Lomonosov Mathematics Olympiad for school students 5-9 grades ELIMINATION STAGE
WINNER:
From 91 points inclusive and above.
PRIZE WINNER:
From 70 points to 90 points inclusive.
## FINAL STAGE
WINNER (Diploma I degree):
Not to be awarded.
PRIZE WINNER (Diploma II degree):
100 points inclusive.
PRIZE WINNER (Diploma III degree):
From 80 points to 99 points inclusive.
[^0]: ${ }^{2}$ Approved at the meeting of the jury of the Lomonosov Mathematics Olympiad for school students. | 16 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. It is known that $x+y+z=2016$ and $\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{7}{224}$. Find $\frac{z}{x+y}+\frac{x}{y+z}+\frac{y}{z+x}$ ANSWER:60. | Solution: Add 1 to each fraction, we get $\frac{z}{x+y}+1+\frac{x}{y+z}+1+\frac{y}{z+x}+1=\frac{x+y+z}{x+y}+$ $\frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}=2016 \cdot\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)=\frac{2016}{32}=63$. | 63 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
6.1. (16 points) In a hut, several inhabitants of the island gathered, some from the Ah tribe, and the rest from the Ukh tribe. The inhabitants of the Ah tribe always tell the truth, while the inhabitants of the Ukh tribe always lie. One of the inhabitants said: "There are no more than 16 of us in the hut," and then added: "We are all from the Ukh tribe." Another said: "There are no more than 17 of us in the hut," and then noted: "Some of us are from the Ah tribe." The third said: "There are five of us in the hut," and, looking around, added: "There are no fewer than three inhabitants from the Ukh tribe among us." How many inhabitants from the Ah tribe are in the hut? | Answer: 15.
Solution. A resident of tribe Ah cannot say "we are all from tribe Ukh," so the first one is from tribe Ukh. Therefore, there are no fewer than 17 people in the hut. So the second one spoke the truth, i.e., he is from tribe Ah. Therefore, there are no more than 17 people in the hut. Thus, there are 17 people in the hut. The third one is from tribe Ukh, as he said there are five of them in total. But since he said there are no fewer than three residents from tribe Ukh, there are no more than two. Two have already been found (the third and the first), so there are exactly two. Then the number of residents from tribe Ah is 15. | 15 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
4. Photographs are archived in the order of their numbering in identical albums, with exactly 4 photographs per page. In this case, the 81st photograph in sequence landed on the 5th page of one of the albums, and the 171st photograph landed on the 3rd page of another. How many photographs can each album hold?
# | # Answer: 32.
Solution. Let $x, y$ be the album numbers in which the 81st and 171st photos are placed, respectively, and $n>4$ be the number of pages in the album. Then $4 n(x-1)+16<81 \leqslant 4 n(x-1)+20, 4 n(y-1)+8<171 \leqslant 4 n(y-1)+12$, i.e., $61 \leqslant 4 n(x-1)<65, 159 \leqslant 4 n(y-1)<163$. Therefore, $n(x-1)=16, n(y-1)=40$. From the first inequality, it follows that $n$ can be $1,2,4,8,16$, from the second $1,2,4,5,8,10,20$, 40. Thus, $n=8, 4 n=32$.
Answer to variant 2: 54.
Answer to variant 3: 40.
Answer to variant $4: 42$. | 32 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
8. Andrei likes all numbers that are not divisible by 3, and Tanya likes all numbers that do not contain digits divisible by 3.
a) How many four-digit numbers are liked by both Andrei and Tanya?
b) Find the total sum of the digits of all such four-digit numbers. | Answer: a) 810; b) 14580.
Solution. a) The required numbers must be composed of the digits $1,2,4,5,7,8$, and according to the divisibility rule by 3, the sum of the digits in each number should not be divisible by three. The digits 1, 4, and 7 (let's call them the digits of set $A$) give a remainder of 1 when divided by 3, while the digits $2,5,8$ (digits of set $B$) give a remainder of 2. Therefore, a number satisfying the condition must be composed in one of the following ways:
1) 4 digits from set $A$ - there are $3^{4}$ such numbers;
2) 4 digits from set $B$ - there are $3^{4}$ such numbers;
3) 3 digits from set $A$ and one digit from set $B$ - there are $4 \cdot 3^{4}$ such numbers;
4) 3 digits from set $B$ and one digit from set $A$ - there are $4 \cdot 3^{4}$ such numbers.
In total, there are $10 \cdot 3^{4}=810$ such numbers.
b) To find the total sum of the digits of all these numbers, we will divide them into pairs: the second number is obtained from the first by replacing all digits according to the principle $1 \leftrightarrow 8,2 \leftrightarrow 7,4 \leftrightarrow 5$. For example, the number 1545 has a pair 8454, the number 5271 has a pair 4728, and so on. The sum of the digits of any pair is $9 \cdot 4$, and the number of such pairs is $\frac{10 \cdot 3^{4}}{2}$. Therefore, the required sum of all digits is $\frac{9 \cdot 4 \cdot 10 \cdot 3^{4}}{2}=20 \cdot 3^{6}=14580$.
Answer to variant 2: a) 160; b) 2880.
Answer to variant 3: a) 810; b) 14580.
Answer to variant 4: a) 160; b) 2880. | 810 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. All natural numbers are divided into "good" and "bad" according to the following rules:
a) From any bad number, you can subtract some natural number not exceeding its half so that the resulting difference becomes "good".
b) From a "good" number, you cannot subtract no more than half of it so that it remains "good".
It is known that the number 1 is "good". Find the nearest "good" number to 2015. | Answer: 2047. Solution. Considering the first few natural numbers, we notice that good numbers have the form $2^{n}-1$ (while $2^{n}, \ldots, 2 n+1-2$ are bad).
We will prove this by mathematical induction. For $n=1$, the statement is given in the condition. Suppose the statement is proven for $n-1$. Consider a number of the form $M=2^{n}+k$, where $k=0,1, \ldots, 2^{n}-2$. Then from such a number, we can subtract $k+1 \leqslant \frac{1}{2}\left(2^{n}+k\right)=\frac{M}{2}$.
On the other hand, consider a number of the form $N=2^{n}-1$. From it, we need to subtract at least $2^{n-1}$, which exceeds $\frac{N}{2}=2^{n-1}-\frac{1}{2}$.
Thus, the nearest good number to 2015 will be the number $2047=2^{11}-1$. | 2047 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. In a convex quadrilateral $A B C D$, the areas of triangles $A B D$ and $B C D$ are equal, and the area of $A C D$ is half the area of $A B D$. Find the length of the segment $C M$, where $M$ is the midpoint of side $A B$, if it is known that $A D=12$. | Answer: $C M=18$. Solution. From the equality of the areas of $A B C$ and $C B D$, it follows that $O$ - the intersection point of the diagonals $A C$ and $B D$ bisects $A C$ (see figure). And from the fact that $S(A C D) = \frac{1}{2} S(A B D)$, it follows that $S(A O D) = \frac{1}{3} S(A O B)$, therefore, $O D = \frac{1}{3} B O = G O$, where $G$ is the point of intersection of the medians of triangle $A B C$.
Thus, $A G C D$ is a parallelogram, so $A D = C G = \frac{2}{3} C M = 12$, from which $C M = 18$.
 | 18 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
1. Find the smallest natural number that is greater than the sum of its digits by 1755 (the year of the founding of Moscow University). | Answer: 1770.
Solution. From the condition, it follows that the desired number cannot consist of three or fewer digits. We will look for the smallest such number in the form $\overline{a b c d}$, where $a, b, c, d$ are digits, and $a \neq 0$. We will form the equation:
$$
\begin{gathered}
\overline{a b c d}=a+b+c+d+1755 \Leftrightarrow 1000 a+100 b+10 c+d=a+b+c+d+1755 \Leftrightarrow \\
\Leftrightarrow 999 a+99 b+9 c=1755 \Leftrightarrow 111 a+11 b+c=195
\end{gathered}
$$
From the last equation, we conclude that the only possible value for the digit $a$ is 1. Next, we get the equation $11 b+c=84$, which means the digit $b$ can only be 7. Finally, we need to find the value of $c=84-11 \cdot 7=7$. Therefore, the desired number is 1770, as it is the smallest among all numbers of the form $\overline{177 d}$. | 1770 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1. There were 21 consecutive natural numbers written on the board. When one of the numbers was erased, the sum of the remaining numbers became 2017. Which number was erased? | Answer: 104.
Solution: Let the numbers on the board be N-10, N-9,..,N, ..., N+10. Their sum is $21 \mathrm{~N}$. When one of these numbers - x - was erased, the sum became 2017, $21 \mathrm{~N}-$ $x=2017$. Therefore, $x=21 N-2017$, since this is one of these numbers, we get $N-10 \leq 21 N-2017 \leq N+10$. Solving the inequalities $\frac{2007}{20} \leq N \leq \frac{2027}{20}$, we get $N$ $=101$, therefore, $x=21 * 101-2017=104$. | 104 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. How many diagonals in a regular 32-sided polygon are not parallel to any of its sides | Answer: 240.
Solution: In a 32-sided polygon, there are $32*(32-3)/2=464$ diagonals in total. We can divide the sides into 16 pairs of parallel sides. It is not hard to notice that if we fix a pair, i.e., 4 vertices, the remaining vertices can be connected in pairs by diagonals parallel to this pair. There will be a total of (32-4)/2 = 14 such diagonals. Therefore, the number of diagonals parallel to any side is $14 * 16=224$. The number of diagonals not parallel to any side is 464-224=240. | 240 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4. For natural numbers $m$ and $n$, it is known that $3 n^{3}=5 m^{2}$. Find the smallest possible value of $m+n$. | Answer: 60.
Solution: Obviously, if $m, n$ contain prime factors other than 3 or 5, then they can be canceled out (and reduce $m+n$).
Let $n=3^{a} \cdot 5^{b}, m=3^{c} \cdot 5^{d}$. Then the condition implies that $3 a+1=2 c, 3 b=2 d+1$.
The smallest possible values are: $a=1, b=1, c=2, d=1$, from which $n=15, m=45$. | 60 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
7. For the function $y=f(x)$, it is known that it is defined and continuous on the entire number line, odd, and periodic with a period of 5, and that $f(-1)=f(2)=-1$. What is the minimum number of roots that the equation $f(x)=0$ can have on the interval [1755; 2017]? Answer: 210. | Solution. Since the function $f$ is odd and defined at zero, we get $f(0)=-f(0)$ $\Rightarrow f(0)=0$. Due to the 5-periodicity, we then have $f(5)=f(0)=0$. Using the oddness again: $f(1)=-f(-1)=1$, and due to the 5-periodicity $f(3)=f(-2)=1, f(4)=$ $f(-1)=-1$. Thus, at points $1, 2, 3$, and $4$, the values of the function are $1, -1, 1$, and $-1$, respectively. Therefore, on each of the three intervals between these points, there is at least one zero of the function $f$. Hence, on the period $[0; 5)$, the function has at least 4 zeros (it is clear that this estimate is achievable: for example, one can take a piecewise-linear function, which will have exactly 4 zeros). On the interval $[1755; 2015)$, the period fits 52 times (on it, there are at least $52 \cdot 4=208$ zeros), plus the zero at the point 2015 and at least one on the interval (2016; 2017). In total, there are at least 210 zeros. | 210 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. Calculate $\sqrt{n}+\sqrt{n+524}$, given that this number is rational and that $n$ is a natural number. | Answer: 262.
Solution. Let the desired number be $a$. We have $\sqrt{n+524}=a-\sqrt{n}, n+524=a^{2}-2 a \sqrt{n}+n$. By the condition, $a$ is rational, so $\sqrt{n}$ is also rational. Therefore, $n=k^{2}, k \in \mathbb{N}$. Then the number $\sqrt{n+524}$ is also rational, so $n+524=m^{2}, m \in \mathbb{N}$. Thus, $m^{2}-k^{2}=524,(m-k)(m+k)=4 \cdot 131$. Note that the numbers $m-k$ and $m+k$ have the same parity, and the number 131 is prime. Therefore, $m-k=2$ and $m+k=2 \cdot 131$. Both equations are satisfied when $m=132, k=130$. Therefore, $a=m+k=262$. | 262 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
8. We consider all possible sets consisting of 2017 different natural numbers, where in each set no number can be represented as the sum of two other numbers in the set. What is the smallest value that the largest number in such a set can take?
Answer: 4032. | Solution. Let for brevity $n=2017$. Consider the following set of $n$ numbers: $n-1, n, n+1, \ldots$, $2 n-3, 2 n-2$. Since $(n-1) + n = 2 n - 1 > 2 n - 2$, no number in this set can equal the sum of two others, meaning the given set satisfies the problem's condition.
Now, let there be an arbitrary set of $n$ natural numbers that satisfy the problem's condition. We will prove that the largest of these numbers $N$ is not less than $2 n - 2$. Suppose $N \leqslant 2 n - 3$. We will prove that in such a set of numbers, there is a pair of numbers less than $N$ whose sum equals $N$. Let's divide all natural numbers less than $N$ into pairs with a sum equal to $N: (1, N-1); (2, N-2), \ldots$. If there are $n-1$ or more such pairs, then the number of numbers less than $N$ will be no less than $2 n - 2$, which is impossible. Therefore, there are no more than $n-2$ such pairs, and there are $n$ numbers in the set. Thus, there will be at least one pair of numbers in the set whose sum equals $N$.
Thus, in any set of $n$ numbers that satisfy the problem's condition, the largest of these numbers is not less than $2 n - 2$ (and this estimate is achievable). In the case $n=2017$, this number is 4032.
Answer to variant 2: 4030. | 4032 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1. In a full container, there are 150 watermelons and melons for a total of 24 thousand rubles, with all the watermelons together costing as much as all the melons. How much does one watermelon cost, given that the container can hold 120 melons (without watermelons) and 160 watermelons (without melons)? | Answer: 100 rubles. Solution. Let there be $x$ watermelons, then there will be $150-x$ melons. If a container can hold 120 melons, then one melon occupies $\frac{1}{120}$ of the container. Similarly, one watermelon occupies $\frac{1}{160}$ of the container. Therefore, if the container is fully loaded with 150 watermelons and melons (and the container is full), then $\frac{x}{160}+\frac{150-x}{120}=1$. From this, $x=120$. So, there were 120 watermelons and 30 melons. If a watermelon costs $a$ rubles, and a melon costs $b$ rubles, then (since the cost of watermelons and melons is the same): $120 a=30 b=12000$. Therefore, $a=100, b=400$. | 100 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. A $3 \times 3$ table needs to be filled with the numbers 2014, 2015, and 2016, such that the sum of the numbers in each row is the same. In how many different ways can this be done? | Answer: 831. Solution. Subtract 2015 from all numbers - the sums will remain the same, and the numbers in the table will take on values of 0 and $\pm 1$. Consider the 27 possible combinations of numbers in one row. Possible values of the sum of these numbers: $\pm 3$ - 1 combination each, $\pm 2$ - 3 combinations each, $\pm 1$ - 6 combinations each, $0-7$ combinations. Then the arrangement specified in the condition can be made in $2 \cdot 1^{3}+2 \cdot 3^{3}+2 \cdot 6^{3}+7^{3}=$ 831 ways. | 831 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. At Andrei's birthday, Yana, who arrived last, gave him a ball, and Eduard, who arrived second to last, gave him a calculator. Testing the calculator, Andrei noticed that the product of the total number of his gifts and the number of gifts he had before Eduard arrived is exactly 16 more than the product of his age and the number of gifts he had before Yana arrived. How many gifts does Andrei have? | Answer: 18. Solution. If $n$ is the number of gifts, and $a$ is Andrei's age, then $n(n-2)=a(n-1)$. From this, $a=\frac{n^{2}-2 n-16}{n-1}=n-1-\frac{17}{n-1}$. Therefore, $n-1=17, a=16$. | 18 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
5. In an equilateral triangle $A B C$, points $A_{1}$ and $A_{2}$ are chosen on side $B C$ such that $B A_{1}=A_{1} A_{2}=A_{2} C$. On side $A C$, a point $B_{1}$ is chosen such that $A B_{1}: B_{1} C=1: 2$. Find the sum of the angles $\angle A A_{1} B_{1}+\angle A A_{2} B_{1}$. | Answer: $30^{\circ}$. Solution. Since $A_{1} B_{1} \| A B$, then $\angle B A A_{1}=\angle A A_{1} B_{1}$. From symmetry, $\angle B A A_{1}=\angle C A A_{2}$. It remains to note that $\angle C B_{1} A_{2}=$ $\angle B_{1} A A_{2}+\angle A A_{2} B_{1}$ as an exterior angle in $\triangle A A_{2} B_{1}$. | 30 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
6. Find the greatest possible value of $\gcd(x+2015 y, y+2015 x)$, given that $x$ and $y$ are coprime numbers. | Answer: $2015^{2}-1=4060224$. Solution. Note that the common divisor will also divide $(x+2015 y)-2015(y+2015 x)=\left(1-2015^{2}\right) x$. Similarly, it divides $\left(1-2015^{2}\right) y$, and since $(x, y)=1$, it divides $\left(1-2015^{2}\right)$. On the other hand, if we take $x=1, y=2015^{2}-2016$, then we get $\gcd(x+2015 y, y+2015 x)=2015^{2}-1$. | 4060224 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. A flea jumps along the number line, and the length of each jump cannot be less than $n$. It starts its movement from the origin and wants to visit all integer points belonging to the segment $[0,2013]$ (and only them!) exactly once. For what greatest value of $n$ will it be able to do this? | Answer: $n=1006$.
Solution: For $n=1006$, a path can be constructed as follows:
$$
0 \rightarrow 1007 \rightarrow 1 \rightarrow 1008 \rightarrow \ldots \rightarrow 1005 \rightarrow 2012 \rightarrow 1006 \rightarrow 2013
$$
We will prove that $n$ cannot be greater than 1006. Indeed, suppose $n \geqslant 1007$. Then the point with coordinate 1007 can only be reached from the start of the segment (point 0). However, if the flea jumps from there to point 1007, it cannot jump back, so it must end its path at this point and will not visit other points on the segment. | 1006 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6. In how many different ways can a chess king move from square $e 1$ to square $h 5$, if it is allowed to move only one square to the right, up, or diagonally to the right-up? | Answer: 129 ways.
Solution: Sequentially (starting from e1) find the number of ways to reach each cell. Each number (except 1) is obtained by summing the neighbors below, to the left, and diagonally left-below.
 | 129 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. How many divisors of the number $2021^{2021}$ have a cube root that is a natural number? | Answer: 454276.
Solution. Since $2021=43 \cdot 47$, all divisors of the number $2021^{2021}$ have the form $43^{\alpha} \cdot 47^{\beta}$, where $\alpha, \beta \in[0 ; 2021]$. In this case, the exact cubes are numbers of the form $43^{3 n} \cdot 47^{3 k}$, where $3 n, 3 k \in[0 ; 2021]$, that is, $n, k \in[0 ; 673]$. There are $674^{2}=454276$ such numbers. | 454276 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1.1. (2 points) From the digits 1, 3, and 5, different three-digit numbers are formed, each of which has all distinct digits. Find the sum of all such three-digit numbers. | Answer: 1998.
Solution. All possible numbers: $135,153,315,351,513,531$. | 1998 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.