Dataset Viewer
problem
stringlengths 15
4.08k
| solution_hint
stringlengths 127
3.05k
| answer
stringlengths 1
44
| problem_type
stringclasses 8
values | source
stringclasses 2
values | solution
stringlengths 13
56
|
|---|---|---|---|---|---|
## A2 ALB
3) If $x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0$, find the value of $x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015$.
| $x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0 \Leftrightarrow(x-\sqrt{3})^{3}=64 \Leftrightarrow(x-\sqrt{3})=4 \Leftrightarrow x-4=\sqrt{3} \Leftrightarrow x^{2}-8 x+16=3 \Leftrightarrow$ $x^{2}-8 x+13=0$
$x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015=\left(x^{2}-8 x+13\right)\left(x^{4}-5 x+9\right)+1898=0+1898=1898$
| 1898 | Algebra | olympiads | \(\boxed{1898}\) |
NT1 SAU
What is the greatest number of integers that can be selected from a set of 2015 consecutive numbers so that no sum of any two selected numbers is divisible by their difference?
| ## Solution:
We take any two chosen numbers. If their difference is 1 , it is clear that their sum is divisible by their difference. If their difference is 2 , they will be of the same parity, and their sum is divisible by their difference. Therefore, the difference between any chosen numbers will be at least 3 . In other words, we can choose at most one number of any three consecutive numbers. This implies that we can choose at most 672 numbers.
Now, we will show that we can choose 672 such numbers from any 2015 consecutive numbers. Suppose that these numbers are $a, a+1, \ldots, a+2014$. If $a$ is divisible by 3 , we can choose $a+1, a+4, \ldots, a+2014$. If $a$ is not divisible by 3 , we can choose $a, a+3, \ldots, a+$ 2013.
| 672 | Number Theory | olympiads | \(\boxed{672}\) |
## A1
For any real number a, let $\lfloor a\rfloor$ denote the greatest integer not exceeding a. In positive real numbers solve the following equation
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=2014
$$
| Obviously $n$ must be positive integer. Now note that $44^{2}=19362000$ than $2014=n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor>2000+44+12=2056$, a contradiction!
So $1950 \leq n \leq 2000$, therefore $\lfloor\sqrt{n}\rfloor=44$ and $\lfloor\sqrt[3]{n}\rfloor=12$. Plugging that into the original equation we get:
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=n+44+12=2014
$$
From which we get $n=1956$, which is the only solution.
| 1956 | Number Theory | olympiads | \(\boxed{1956}\) |
## C2
In a country with $n$ cities, all direct airlines are two-way. There are $r>2014$ routes between pairs of different cities that include no more than one intermediate stop (the direction of each route matters). Find the least possible $n$ and the least possible $r$ for that value of $n$.
| Denote by $X_{1}, X_{2}, \ldots X_{n}$ the cities in the country and let $X_{i}$ be connected to exactly $m_{i}$ other cities by direct two-way airline. Then $X_{i}$ is a final destination of $m_{i}$ direct routes and an intermediate stop of $m_{i}\left(m_{i}-1\right)$ non-direct routes. Thus $r=m_{1}^{2}+\ldots+m_{n}^{2}$. As each $m_{i}$ is at most $n-1$ and $13 \cdot 12^{2}<2014$, we deduce $n \geq 14$.
Consider $n=14$. As each route appears in two opposite directions, $r$ is even, so $r \geq 2016$. We can achieve $r=2016$ by arranging the 14 cities uniformly on a circle connect (by direct two-way airlines) all of them, except the diametrically opposite pairs. This way, there are exactly $14 \cdot 12^{2}=2016$ routes.
| 2016 | Combinatorics | olympiads | \(\boxed{2016}\) |
Problem A2. Determine all four digit numbers $\overline{a b c d}$ such that
$$
a(a+b+c+d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)\left(a^{6}+2 b^{6}+3 c^{6}+4 d^{6}\right)=\overline{a b c d}
$$
| From $\overline{a b c d}\overline{1 b c d}=(1+b+c+d)\left(1+b^{2}+c^{2}+d^{2}\right)\left(1+2 b^{6}+3 c^{6}+4 d^{6}\right) \geq$ $(b+1)\left(b^{2}+1\right)\left(2 b^{6}+1\right)$, so $b \leq 2$. Similarly one gets $c\overline{2 b c d}=2(2+b+c+d)\left(4+b^{2}+c^{2}+d^{2}\right)\left(64+2 b^{6}+3 c^{6}+4 d^{6}\right) \geq$ $2(b+2)\left(b^{2}+4\right)\left(2 b^{6}+64\right)$, imposing $b \leq 1$. In the same way one proves $c<2$ and $d<2$. By direct check, we find out that 2010 is the only solution.
| 2010 | Number Theory | olympiads | \(\boxed{2010}\) |
C2. The natural numbers from 1 to 50 are written down on the blackboard. At least how many of them should be deleted, in order that the sum of any two of the remaining numbers is not a prime?
| Notice that if the odd, respectively even, numbers are all deleted, then the sum of any two remaining numbers is even and exceeds 2 , so it is certainly not a prime. We prove that 25 is the minimal number of deleted numbers. To this end, we group the positive integers from 1 to 50 in 25 pairs, such that the sum of the numbers within each pair is a prime:
$$
\begin{aligned}
& (1,2),(3,4),(5,6),(7,10),(8,9),(11,12),(13,16),(14,15),(17,20) \\
& (18,19),(21,22),(23,24),(25,28),(26,27),(29,30),(31,36),(32,35) \\
& (33,34),(37,42),(38,41),(39,40),(43,46),(44,45),(47,50),(48,49)
\end{aligned}
$$
Since at least one number from each pair has to be deleted, the minimal number is 25 .
| 25 | Number Theory | olympiads | \(\boxed{25}\) |
C3 a) In how many ways can we read the word SARAJEVO from the table below, if it is allowed to jump from cell to an adjacent cell (by vertex or a side) cell?
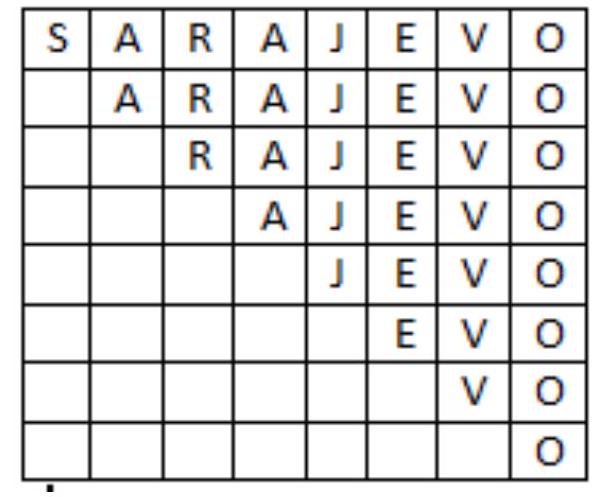
b) After the letter in one cell was deleted, only 525 ways to read the word SARAJEVO remained. Find all possible positions of that cell.
| In the first of the tables below the number in each cell shows the number of ways to reach that cell from the start (which is the sum of the quantities in the cells, from which we can come), and in the second one are the number of ways to arrive from that cell to the end (which is the sum of the quantities in the cells, to which we can go).
a) The answer is 750 , as seen from the second table.
b) If we delete the letter in a cell, the number of ways to read SARAJEVO will decrease by the product of the numbers in the corresponding cell in the two tables. As $750-525=225$, this product has to be 225. This happens only for two cells on the third row. Here is the table with the products:
| 750 | Combinatorics | olympiads | \(\boxed{750}\) |
A4 Let $x, y$ be positive real numbers such that $x^{3}+y^{3} \leq x^{2}+y^{2}$. Find the greatest possible value of the product $x y$.
| ## Solution 1
We have $(x+y)\left(x^{2}+y^{2}\right) \geq(x+y)\left(x^{3}+y^{3}\right) \geq\left(x^{2}+y^{2}\right)^{2}$, hence $x+y \geq x^{2}+y^{2}$. Now $2(x+y) \geq(1+1)\left(x^{2}+y^{2}\right) \geq(x+y)^{2}$, thus $2 \geq x+y$. Because $x+y \geq 2 \sqrt{x y}$, we will obtain $1 \geq x y$. Equality holds when $x=y=1$.
So the greatest possible value of the product $x y$ is 1 .
| 1 | Inequalities | olympiads | \(\boxed{1}\) |
87.3. Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
| Since $f(n)=n^{2}$ is a function satisfying the conditions of the problem, the smallest posiible $a$ is at most 4. Assume $a=3$. It is easy to prove by induction that $f\left(n^{k}\right)=f(n)^{k}$ for all $k \geq 1$. So, taking into account that $f$ is strictly increasing, we get
$$
\begin{gathered}
f(3)^{4}=f\left(3^{4}\right)=f(81)>f(64)=f\left(2^{6}\right)=f(2)^{6} \\
=3^{6}=27^{2}>25^{2}=5^{4}
\end{gathered}
$$
as well as
$$
\begin{aligned}
& f(3)^{8}=f\left(3^{8}\right)=f(6561)<f(8192) \\
& \quad=f\left(2^{13}\right)=f(2)^{13}=3^{13}<6^{8}
\end{aligned}
$$
So we arrive at $5<f(3)<6$. But this is not possible, since $f(3)$ is an integer. So $a=4$.
| 4 | Algebra | olympiads | \(\boxed{4}\) |
88.1. The positive integer $n$ has the following property: if the three last digits of $n$ are removed, the number $\sqrt[3]{n}$ remains. Find $n$.
| If $x=\sqrt[3]{n}$, and $y, 0 \leq y1000$, and $x>31$. On the other hand, $x^{3}<1000 x+1000$, or $x\left(x^{2}-1000\right)<1000$. The left hand side of this inequality is an increasing function of $x$, and $x=33$ does not satisfy the inequality. So $x<33$. Since $x$ is an integer, $x=32$ and $n=32^{3}=32768$.
| 32768 | Number Theory | olympiads | \(\boxed{32768}\) |
91.1. Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
| We first show that all numbers $2^{5^{k}}$ are of the form $100 p+32$. This can be shown by induction. The case $k=1$ is clear $\left(2^{5}=32\right)$. Assume $2^{5^{k}}=100 p+32$. Then, by the binomial formula,
$$
2^{5^{k+1}}=\left(2^{5^{k}}\right)^{5}=(100 p+32)^{5}=100 q+32^{5}
$$
and
$$
\begin{gathered}
(30+2)^{5}=30^{5}+5 \cdot 30^{4} \cdot 2+10 \cdot 30^{3} \cdot 4+10 \cdot 30^{2} \cdot 8+5 \cdot 30 \cdot 16+32 \\
=100 r+32
\end{gathered}
$$
So the last two digits of the sum in the problem are the same as the last digits of the number $1991 \cdot 32$, or 12 .
| 12 | Number Theory | olympiads | \(\boxed{12}\) |
97.1. Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
| Let $0<a_{1}<a_{2}<\ldots<a_{7}$ be the elements of the set $A$. If $\left(a_{i}, a_{j}, a_{k}\right)$ is a triple of the kind required in the problem, then $a_{i}<a_{j}<a_{i}+a_{j}=a_{k}$. There are at most $k-1$ pairs $\left(a_{i}, a_{j}\right)$ such that $a_{i}+a_{j}=a_{k}$. The number of pairs satisfying $a_{i}<a_{j}$ is at most $\left\lfloor\frac{k-1}{2}\right\rfloor$. The total number of pairs is at most
$$
\sum_{k=3}^{7}\left\lfloor\frac{k-1}{2}\right\rfloor=1+1+2+2+3=9
$$
The value 9 can be reached, if $A=\{1,2, \ldots, 7\}$. In this case the triples $(1,2,3),(1,3,4)$, $(1,4,5),(1,5,6),(1,6,7),(2,3,5),(2,4,6),(2,5,7)$, and $(3,4,7)$ satisfy the conditions of the problem.
| 9 | Combinatorics | olympiads | \(\boxed{9}\) |
01.3. Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
| Write
$$
\begin{gathered}
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2} \\
=x(x-1)\left(x^{6}+2 x^{4}+3 x^{2}+4\right)+\frac{5}{2}
\end{gathered}
$$
If $x(x-1) \geq 0$, i.e. $x \leq 0$ or $x \geq 1$, the equation has no roots. If $0x(x-1)=\left(x-\frac{1}{2}\right)^{2}-\frac{1}{4} \geq-\frac{1}{4}$ and $x^{6}+2 x^{4}+3 x+4<1+2+3+4=10$. The value of the left-hand side of the equation now is larger than $-\frac{1}{4} \cdot 10+\frac{5}{2}=0$. The equation has no roots in the interval $(0,1)$ either.
| 0 | Algebra | olympiads | \(\boxed{0}\) |
05.1. Find all positive integers $k$ such that the product of the digits of $k$, in the decimal system, equals
$$
\frac{25}{8} k-211
$$
| Let
$$
a=\sum_{k=0}^{n} a_{k} 10^{k}, \quad 0 \leq a_{k} \leq 9, \text { for } 0 \leq k \leq n-1,1 \leq a_{n} \leq 9
$$
Set
$$
f(a)=\prod_{k=0}^{n} a_{k}
$$
Since
$$
f(a)=\frac{25}{8} a-211 \geq 0
$$
$a \geq \frac{8}{25} \cdot 211=\frac{1688}{25}>66$. Also, $f(a)$ is an integer, and $\operatorname{gcf}(8,25)=1$, so $8 \mid a$. On the other hand,
$$
f(a) \leq 9^{n-1} a_{n} \leq 10^{n} a_{n} \leq a
$$
So
$$
\frac{25}{8} a-211 \leq a
$$
or $a \leq \frac{8}{17} \cdot 211=\frac{1688}{17}<100$. The only multiples of 8 between 66 and 100 are $72,80,88$, and 96. Now $25 \cdot 9-211=17=7 \cdot 2,25 \cdot 10-211=39 \neq 8 \cdot 0,25 \cdot 11-211=64=8 \cdot 8$, and $25 \cdot 12-211=89 \neq 9 \cdot 6$. So 72 and 88 are the numbers asked for.
| 7288 | Number Theory | olympiads | \(\boxed{7288}\) |
XXV - I - Task 1
During World War I, a battle took place near a certain castle. One of the shells destroyed a statue of a knight with a spear standing at the entrance to the castle. This happened on the last day of the month. The product of the day of the month, the month number, the length of the spear expressed in feet, half the age of the battery commander firing at the castle expressed in years, and half the time the statue stood expressed in years equals 451,066. In which year was the statue erected? | The last day of the month can only be $28$, $29$, $30$, or $31$. Of these numbers, only $29$ is a divisor of the number $451,066 = 2 \cdot 7 \cdot 11 \cdot 29 \cdot 101$. Therefore, the battle took place on February $29$ in a leap year. During World War I, only the year $1916$ was a leap year. From the problem statement, it follows that a divisor of the number $7 \cdot 11 \cdot 101$ is half the age of the battery commander. Only the number $11$ satisfies this condition, so the battery commander was $22$ years old. The length of the pike is a divisor of the number $7 \cdot 101$. Therefore, the pike was $7$ feet long. Thus, half the time the statue stood is $101$ years. It was erected $202$ years before the year $1916$, i.e., in the year $1714$. | 1714 | Logic and Puzzles | olympiads | \(\boxed{1714}\) |
XII OM - II - Task 4
Find the last four digits of the number $ 5^{5555} $. | \spos{1} We will calculate a few consecutive powers of the number $ 5 $ starting from $ 5^4 $:
It turned out that $ 5^8 $ has the same last four digits as $ 5^4 $, and therefore the same applies to the numbers $ 5^9 $ and $ 5^5 $, etc., i.e., starting from $ 5^4 $, two powers of the number $ 5 $, whose exponents differ by a multiple of $ 4 $, have the same last four digits. The number $ 5^{5555} = 5^{4\cdot 1388+3} $ therefore has the same last $ 4 $ digits as the number $ 5^7 $, i.e., the digits $ 8125 $. | 8125 | Number Theory | olympiads | \(\boxed{8125}\) |
XXXIX OM - I - Problem 1
For each positive number $ a $, determine the number of roots of the polynomial $ x^3+(a+2)x^2-x-3a $. | Let's denote the considered polynomial by $ F(x) $. A polynomial of the third degree has at most three real roots. We will show that the polynomial $ F $ has at least three real roots - and thus has exactly three real roots (for any value of the parameter $ a > 0 $).
It is enough to notice that
If a continuous function with real values takes values of different signs at two points, then at some point in the interval bounded by these points, it takes the value zero (Darboux property).
Hence, in each of the intervals $ (-a-3; -2) $, $ (-2; 0) $, $ (0; 2) $, there is a root of the polynomial $ F $. | 3 | Algebra | olympiads | \(\boxed{3}\) |
V OM - I - Task 2
Investigate when the sum of the cubes of three consecutive natural numbers is divisible by $18$. | Let $ a - 1 $, $ a $, $ a + 1 $, be three consecutive natural numbers; the sum of their cubes
can be transformed in the following way:
Since one of the numbers $ a - 1 $, $ a $, $ a + 1 $ is divisible by $ 3 $, then one of the numbers $ a $ and $ (a + 1) (a - 1) + 3 $ is also divisible by $ 3 $. Therefore, the sum $ S $ of the cubes of three consecutive natural numbers is always divisible by $ 9 $.
The sum $ S $ is thus divisible by $ 18 = 9 \cdot 2 $ if and only if it is divisible by $ 2 $. Since $ S = 3a^3 + 6a $, $ S $ is even if and only if $ a $ is even, i.e., when $ a - 1 $ is odd. Hence, the conclusion:
The sum of the cubes of three consecutive natural numbers is divisible by $ 18 $ if and only if the first of these numbers is odd. | 3 | Number Theory | olympiads | \(\boxed{3}\) |
L OM - I - Problem 11
In an urn, there are two balls: a white one and a black one. Additionally, we have 50 white balls and 50 black balls at our disposal. We perform the following action 50 times: we draw a ball from the urn, and then return it to the urn along with one more ball of the same color as the drawn ball. After completing these actions, we have 52 balls in the urn. What is the most probable number of white balls in the urn? | Let $ P(k,n) $, where $ 1 \leq k\leq n-1 $, denote the probability of the event that when there are $ n $ balls in the urn, exactly $ k $ of them are white. Then
Using the above relationships, we prove by induction (with respect to $ n $) that $ P(k,n) = 1/(n-1) $ for $ k = 1,2,\ldots,n-1 $. In particular
Therefore, each possible number of white balls after $ 50 $ draws (from $ 1 $ to $ 51 $) is equally likely. | 51 | Combinatorics | olympiads | \(\boxed{51}\) |
XXVI - I - Task 1
At the ball, there were 42 people. Lady $ A_1 $ danced with 7 gentlemen, Lady $ A_2 $ danced with 8 gentlemen, ..., Lady $ A_n $ danced with all the gentlemen. How many gentlemen were at the ball? | The number of ladies at the ball is $ n $, so the number of gentlemen is $ 42-n $. The lady with number $ k $, where $ 1 \leq k \leq n $, danced with $ k+6 $ gentlemen. Therefore, the lady with number $ n $ danced with $ n+ 6 $ gentlemen. These were all the gentlemen present at the ball. Thus, $ 42-n = n + 6 $. Solving this equation, we get $ n = 18 $. The number of gentlemen at the ball is therefore $ 42-18 = 24 $. | 24 | Combinatorics | olympiads | \(\boxed{24}\) |
1. When purchasing goods for an amount of no less than 1000 rubles, the store provides a discount on subsequent purchases of $50 \%$. Having 1200 rubles in her pocket, Dasha wanted to buy 4 kg of strawberries and 6 kg of sugar. In the store, strawberries were sold at a price of 300 rubles per kg, and sugar - at a price of 30 rubles per kg. Realizing that she didn't have enough money for the purchase, Dasha still managed to buy what she intended. How did she do it? | First purchase: 3 kg of strawberries, 4 kg of sugar. Its cost is $300 \times 3 + 4 \times 30 = 1020$ rubles. Second purchase: 1 kg of strawberries, 2 kg of sugar. With a $50\%$ discount, its price is $(300 + 60) \cdot 0.5 = 180$ rubles. The total amount of both purchases is $1200$ rubles. | 1200 | Logic and Puzzles | olympiads | \(\boxed{1200}\) |
2. The number $A$ in decimal form is represented as $A=\overline{7 a 631 b}$, where $a, b$ are non-zero digits. The number $B$ is obtained by summing all distinct six-digit numbers, including $A$, that are formed by cyclic permutations of the digits of $A$ (the first digit moves to the second position, the second to the third, and so on, with the last digit moving to the first position). How many numbers $A$ exist such that $B$ is divisible by 121? Find the largest such $A$. | Solution. The sum of the digits of number $A$ and the numbers obtained from $A$ by cyclic permutations of its digits is $a+b+17$. After summing these numbers (there are 6 of them), in each digit place of number $B$ we get
$a+b+17$, so $B=(a+b+17)\left(10^{5}+10^{4}+10^{3}+10^{2}+10+1\right)=(a+b+17) \cdot 111111$. Since
$111111=3 \cdot 7 \cdot 11 \cdot 13 \cdot 37$, $B$ is divisible by 121 if and only if $a+b+17$ is divisible by 11. Since $a$ and $b$ are digits, there are only two possible cases: $a+b=5$ and $a+b=16$. From this, we find the possible pairs of $a$ and $b$: $a=1, b=4 ; a=2, b=3 ; a=3, b=2 ; a=4, b=1 ; a=7, b=9 ; a=8, b=8 ; a=9, b=7$. Thus, 7 numbers satisfy the condition of the problem. The largest number is obtained when $a=9, b=7$. It is 796317. | 796317 | Number Theory | olympiads | \(\boxed{796317}\) |
1. Find the number of divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3. Find the sum of such divisors. | Solution. Among the divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3, the number 2 can be chosen with exponents $0,1,2,3$ (4 options), the number 3 - with exponents 1,2 (2 options), and the number 5 - with exponents $0,1,2$ (3 options). Therefore, the total number of divisors is $4 \cdot 2 \cdot 3=24$. The sum of the divisors of the number $b=2^{3} \cdot 5^{2}$ is $(1+2+4+8)(1+5+25)=465$. Then the sum of the divisors of the number $a$, which are divisible by 3, is $\left(3+3^{2}\right) \cdot 465=12 \cdot 465=5580$. | 5580 | Number Theory | olympiads | \(\boxed{5580}\) |
3. How many three-digit positive numbers $x$ exist that are divisible by 3 and satisfy the equation $GCD(15, GCD(x, 20))=5$? Find the largest one. | Solution. Since 20 is not divisible by 3, $NOD(x, 20)$ is also not divisible by 3. Therefore, the equation $NOD(15, NOD(x, 20))=5$ is equivalent to the condition that $NOD(x, 20)$ is divisible by 5, which is possible if and only if $x$ is divisible by 5. Thus, the condition of the problem is equivalent to $x$ being divisible by 5 and by 3, that is, $x$ is divisible by 15. Therefore, $x$ can be written as $x=15m, m=1,2 \ldots$. The smallest three-digit $x=105$ is obtained when $m=7$, and the largest three-digit $x=990$ is obtained when $m=66$, making a total of 60 numbers. | 60 | Number Theory | olympiads | \(\boxed{60}\) |
5. A football is sewn from 256 pieces of leather: white ones in the shape of hexagons and black ones in the shape of pentagons. Black pentagons only border white hexagons, and any white hexagon borders three black pentagons and three white hexagons. Find the number of white hexagons on the football. | Criteria for checking works, 7th grade
Preliminary round of the sectoral physics and mathematics olympiad for schoolchildren "Rosatom", mathematics
# | 160 | Combinatorics | olympiads | \(\boxed{160}\) |
1. (10 points). Tourist Nikolai Petrovich was late by $\Delta t=5$ minutes for the departure of his riverboat, which had set off downstream. Fortunately, the owner of a fast motorboat agreed to help Nikolai Petrovich. Catching up with the riverboat and disembarking the unlucky tourist, the motorboat immediately set off on its return journey. How much time passed from the departure of the motorboat until its return? Assume that the speed of the riverboat relative to the water is $k=3$ times the speed of the river current, and the speed of the motorboat is $n=5$ times the speed of the river current. | $s=\left(3 v_{\mathrm{T}}+v_{\mathrm{T}}\right) \cdot\left(t_{1}+\Delta t\right)=\left(5 v_{\mathrm{T}}+v_{\mathrm{T}}\right) \cdot t_{1} \rightarrow 4 \Delta t=2 t_{1} \rightarrow t_{1}=2 \Delta t=10$ min $t_{2}=\frac{s}{5 v_{\mathrm{T}}-v_{\mathrm{T}}}=\frac{6 v_{\mathrm{T}} \cdot t_{1}}{4 v_{\mathrm{T}}}=\frac{3}{2} t_{1}=3 \Delta t=15$ min $\rightarrow$ $T=t_{1}+t_{2}=5 \Delta t=25$ min | 25 | Algebra | olympiads | \(\boxed{25}\) |
2. (15 points) A satellite is launched vertically from the pole of the Earth at the first cosmic speed. To what maximum distance from the Earth's surface will the satellite travel? (The acceleration due to gravity at the Earth's surface $g=10 \mathrm{m} / \mathrm{c}^{2}$, radius of the Earth $R=6400$ km). | According to the law of conservation of energy: $\frac{m v_{I}^{2}}{2}-\frac{\gamma m M}{R}=-\frac{\gamma m M}{R+H}$
The first cosmic speed $v_{I}=\sqrt{g R}$
The acceleration due to gravity at the surface $g=\frac{\gamma M}{R^{2}}$
Then $\frac{m g R}{2}-m g R=-\frac{m g R^{2}}{R+H}$
Finally, $H=R=6400$ km.
(15 points) | 6400 | Algebra | olympiads | \(\boxed{6400}\) |
3. (15 points) Determine the mass $m$ of helium needed to fill an empty balloon of mass $m_{1}=10$ g so that the balloon will rise. Assume the temperature and pressure of the gas in the balloon are equal to the temperature and pressure of the air. The molar mass of helium $M_{\mathrm{r}}=4$ g/mol, the molar mass of air $M_{\mathrm{B}}=29$ g/mol. | For the balloon to take off, the condition is $F_{\text {Arch }}=\left(m+m_{1}\right) g$
$F_{\text {Arch }}=\rho_{0} g V$
From the Clapeyron-Mendeleev equation, the density of air is
$\rho_{0}=\frac{P_{0} M_{\mathrm{B}}}{R T_{0}}, \quad$ and the volume of the balloon $V=\frac{m}{M_{\mathrm{r}}} \frac{R T_{0}}{P_{0}}$
Then $m \frac{M_{\mathrm{B}}}{M_{\mathrm{r}}}=\left(m+m_{1}\right)$
Finally, $m=\frac{m_{1} M_{\mathrm{r}}}{M_{\mathrm{B}}-M_{\mathrm{r}}}=1.6$ g.
(15 points) | 1.6 | Algebra | olympiads | \(\boxed{1.6}\) |
4. (15 points) Carefully purified water can be supercooled to a temperature below $0^{\circ}$. However, if a crystal of ice is thrown into it, the water will immediately begin to freeze. What fraction of water supercooled to $-10^{\circ} \mathrm{C}$ in a thermos will freeze if a small ice chip is thrown into it? The specific heat capacity of water $c=4200$ J/(kg$\cdot$K), the latent heat of fusion of ice $\lambda=330$ kJ/kg. | A small ice crystal becomes a center of crystallization. The heat released during crystallization goes to heating the water. Eventually, thermal equilibrium is established at $t=0^{\circ} \mathrm{C}$.
From the heat balance equation $\quad \lambda m_{\text{ice}}=c m_{\text{water}} \Delta t$
Finally $\quad \frac{m_{\text{ice}}}{m_{\text{water}}}=\frac{c \Delta t}{\lambda}=0.13$.
(15 points)
Solutions. | 0.13 | Other | olympiads | \(\boxed{0.13}\) |
5. (25 points) Six resistors with resistances $R_{1}=1$ Ohm, $R_{2}=2$ Ohm, $R_{3}=3$ Ohm, $R_{4}=4$ Ohm, $R_{5}=5$ Ohm, and $R_{6}=6$ Ohm are connected in series and form a loop. A source of constant voltage is connected to the resulting circuit such that the resistance between its terminals is maximized. The voltage of the source is $U=12 \mathrm{~V}$. Find the power $P_{3}$ dissipated on the resistor $R_{3}$. | When connecting a source to any two contacts, the external circuit will represent two parallel branches. Then the total resistance of the circuit is
$R_{\text {total }}=\frac{R_{I} R_{I I}}{R_{I}+R_{I I}}$
For any method of connection, the sum of the resistances in the branches is the same (21 Ohms). The total resistance will be the greatest when the product of the resistances in the branches is maximized. (See the diagram). The power dissipated in the third resistor is
$P_{3}=I_{3}^{2} R_{3}=\frac{U^{2} R_{3}}{\left(R_{1}+R_{2}+R_{3}+R_{4}\right)^{2}}=4.32$ W.
(25 points) | 4.32 | Algebra | olympiads | \(\boxed{4.32}\) |
6. (15 points) Looking down from the edge of the stream bank, Vovochka decided that the height of his rubber boots would be enough to cross the stream. However, after crossing, Vovochka got his legs wet up to his knees ($H=52$ cm). Estimate the height $h$ of Vovochka's boots. Assume the depth of the stream is constant, and the refractive index of water $n=1.33$.
Rector of SPbPU

A.I. Rudskoy S.A. Staroytov
## Instructions for Evaluating Final Round Solutions of the Polytechnic Physics Olympiad
The version given to the participant contains 6 problems of varying difficulty.
The evaluation of the work is based on the points received for each individual problem.
The score for solving each problem in the version is one of the following coefficients:
1.0 - the problem is solved correctly;
0.8 - the problem is solved correctly and the answer is given in a general form; there is an error in the unit of measurement of the obtained physical quantity or an arithmetic error;
0.6 - the problem is not fully solved; all necessary physical relationships for solving the problem are present; there is an error in algebraic transformations;
0.4 - the problem is not fully solved; some physical relationships necessary for solving the problem are missing;
0.2 - the problem is not solved; the work contains only some notes related to solving the problem or describing the phenomenon considered in the problem;
0.0 - the solution to the problem or any notes related to it are absent in the work.
The coefficient is entered in the first column "For the Teacher" of the "Answer Sheet". In the second column of the section, the score is entered, which is the product of the coefficient received for the solution and the maximum score for the given problem.
The obtained scores are summed and entered in the "Total" row.
Table for converting coefficients to points.
| \multirow{coefficient}{max points}{} | 10 | 15 | 20 | 25 |
| :---: | :---: | :---: | :---: | :---: |
| 1 | 10 | 15 | 20 | 25 |
| 0.8 | 8 | 12 | 16 | 20 |
| 0.6 | 6 | 9 | 12 | 15 |
| 0.4 | 4 | 6 | 8 | 10 |
| 0.2 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 | | From the figure
$\frac{d}{h}=\operatorname{tg} \alpha ; \quad \frac{d}{H}=\operatorname{tg} \beta ; \quad \frac{H}{h}=\frac{\operatorname{tg} \alpha}{\operatorname{tg} \beta}$
Since all the information about the bottom of the stream falls into the space limited by the eye's pupil, all angles are small: $\operatorname{tg} \alpha \approx \sin \alpha ; \operatorname{tg} \beta \approx \sin \beta$
Then $\frac{H}{h}=\frac{\sin \alpha}{\sin \beta}=n$
$h=\frac{H}{n}=39 \mathrm{~cm}$.
(15 points) | 39 | Other | olympiads | \(\boxed{39}\) |
2. (15 points) A wooden cube with edge $\ell=30$ cm floats in a lake. The density of wood $\quad \rho=750 \mathrm{kg} / \mathrm{m}^{3}, \quad$ the density of water $\rho_{0}=1000 \mathrm{kg} / \mathrm{m}^{3}$. What is the minimum work required to completely pull the cube out of the water? | In equilibrium $m g=\rho_{0} g \frac{3}{4} \ell^{3}$
External minimal force at each moment in time
$$
F=m g-F_{\mathrm{Apx}}=\rho_{0} g \frac{3}{4} \ell^{3}-\rho_{0} g \ell^{2}\left(\frac{3}{4} \ell-x\right)=\rho_{0} g \ell^{2} x,
$$
where $x$ is the height of the lift at that moment. The external force depends linearly on the height of the lift, so the work done by this force is equal to the area of the figure (triangle) on the $F(x)$ diagram
$A_{\text {min }}=\frac{1}{2} \frac{3}{4} \rho_{0} g \ell^{3} \frac{3}{4} \ell=\frac{9}{32} \rho_{0} g \ell^{4}=22.8$ J.
(15 points) | 22.8 | Algebra | olympiads | \(\boxed{22.8}\) |
# 18. Problem 18
The owner of an apartment rents it out for five years and receives 240,000 rubles from tenants at the end of each year. The owner does not spend the rental income but saves it in a term deposit with an annual interest rate of $10\%$ (capitalization occurs once at the end of the year). What amount will the owner have in the account after five years? | Write the answer as a number without spaces, without units of measurement, and without any symbols (rounding to the nearest whole number if necessary).
# | 159383 | Algebra | olympiads | \(\boxed{159383}\) |
Problem 1. Seven students in the class receive one two every two days of study, and nine other students receive one two every three days each. The rest of the students in the class never receive twos. From Monday to Friday, 30 new twos appeared in the journal. How many new twos will appear in the class journal on Saturday? | Over the period from Monday to Saturday (six days), in the journal, there will be 3 new twos from each student of the first group (seven people) and 2 new twos from each of the 9 students of the second group. The total number of new twos for the school week is $7 \cdot 3 + 9 \cdot 2 = 39$. Then, on Saturday, the journal will have $39 - 30 = 9$ new twos. | 9 | Logic and Puzzles | olympiads | \(\boxed{9}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+11 x+23$. | Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+11 x+23>0 \Leftrightarrow-\frac{1}{4}(x+2)(x-46)>0$, from which $-2<x<46$. On this interval, there are 45 natural values of $x: x=1, x=2, \ldots, x=45$. In this interval, $y$ takes integer values only for even $x$ - a total of 22 possibilities. Thus, we get 22 points belonging to the parabola, both of whose coordinates are natural numbers. | 22 | Algebra | olympiads | \(\boxed{22}\) |
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can be repeated) so that the resulting 12-digit number is divisible by 45. In how many ways can this be done? | For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We will choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and then select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $2 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=13122$. | 13122 | Combinatorics | olympiads | \(\boxed{13122}\) |
1. Find the number of points in the $x O y$ plane that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{4}+3 x+\frac{253}{4}$. | Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+3 x+\frac{253}{4}>0 \Leftrightarrow-\frac{1}{4}(x+11)(x-23)>0$, from which $-11<x<23$. On this interval, there are 22 natural values of $x: x=1, x=2, \ldots, x=22$. During this interval, $y$ takes integer values only for even $x$ - a total of 11 possibilities. Therefore, we get 11 points belonging to the parabola, both of whose coordinates are natural numbers. | 11 | Algebra | olympiads | \(\boxed{11}\) |
3. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 18. In how many ways can this be done? | For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6$ or 8 (5 ways).
To ensure divisibility by nine, we proceed as follows. Choose three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0, 1, 2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $5 \cdot 9 \cdot 9 \cdot 9 \cdot 1 = 3645$. | 3645 | Combinatorics | olympiads | \(\boxed{3645}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+9 x+19$. | Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+9 x+19>0 \Leftrightarrow-\frac{1}{4}(x+2)(x-38)>0$, from which $-2<x<38$. On this interval, there are 37 natural values of $x: x=1, x=2, \ldots, x=37$. In this interval, $y$ takes integer values only for even $x$ - a total of 18 possibilities. Thus, we get 18 points belonging to the parabola, both of whose coordinates are natural numbers. | 18 | Algebra | olympiads | \(\boxed{18}\) |
3. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 45. In how many ways can this be done? | For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We select three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and choose the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that there are $2 \cdot 9 \cdot 9 \cdot 9 \cdot 1=1458$ ways. | 1458 | Combinatorics | olympiads | \(\boxed{1458}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+5 x+39$. | Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+5 x+39>0 \Leftrightarrow-\frac{1}{4}(x+6)(x-26)>0$, from which $-6<x<26$. On this interval, there are 25 natural values of $x: x=1, x=2, \ldots, x=25$. In this interval, $y$ takes integer values only for even $x$ - a total of 12 possibilities. Therefore, we get 12 points belonging to the parabola, both of whose coordinates are natural numbers. | 12 | Algebra | olympiads | \(\boxed{12}\) |
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $1,2,3,4,5,6,7,8,9$ (digits can repeat) so that the resulting 12-digit number is divisible by 18. In how many ways can this be done? | For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $2, 4, 6$ or 8 (4 ways).
To ensure divisibility by nine, we proceed as follows. Choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $4 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=26244$. | 26244 | Combinatorics | olympiads | \(\boxed{26244}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+13 x+42$. | Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+13 x+42>0 \Leftrightarrow-\frac{1}{3}(x+3)(x-42)>0$, from which $-3<x<42$. On this interval, there are 41 natural values of $x: x=1, x=2, \ldots, x=41$. In this case, $y$ takes integer values only when $x$ is divisible by 3 - a total of 13 possibilities. Thus, we get 13 points belonging to the parabola, both of whose coordinates are natural numbers. | 13 | Algebra | olympiads | \(\boxed{13}\) |
2. Find the value of the expression $\frac{a}{b}+\frac{b}{a}$, where $a$ and $b$ are the largest and smallest roots of the equation $x^{3}-7 x^{2}+7 x=1$, respectively. | The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-7\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-7 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-6 x+1\right)=0,
$$
from which $x=1$ or $x=3 \pm \sqrt{8}$. The largest root is $a=3+\sqrt{8}$, and the smallest is $-b=3-\sqrt{8}$. Then
$$
\frac{a}{b}+\frac{b}{a}=\frac{3+\sqrt{8}}{3-\sqrt{8}}+\frac{3-\sqrt{8}}{3+\sqrt{8}}=\frac{(3+\sqrt{8})^{2}+(3-\sqrt{8})^{2}}{(3+\sqrt{8})(3-\sqrt{8})}=\frac{2(9+8)}{1}=34
$$ | 34 | Algebra | olympiads | \(\boxed{34}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+7 x+54$. | Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+7 x+54>0 \Leftrightarrow-\frac{1}{3}(x+6)(x-27)>0$, from which $-6<x<27$. On this interval, there are 26 natural values of $x: x=1, x=2, \ldots, x=26$. In this interval, $y$ takes integer values only when $x$ is divisible by 3 - a total of 8 possibilities. Therefore, we get 8 points on the parabola, both of whose coordinates are natural numbers. | 8 | Algebra | olympiads | \(\boxed{8}\) |
2. Find the value of the expression $\frac{p}{q}+\frac{q}{p}$, where $p$ and $q$ are the largest and smallest roots of the equation $x^{3}+6 x^{2}+6 x=-1$, respectively. | The given equation is equivalent to the following
$$
\left(x^{3}+1\right)+6\left(x^{2}+x\right)=0 \Leftrightarrow(x+1)\left(x^{2}-x+1\right)+6 x(x+1)=0 \Leftrightarrow(x+1)\left(x^{2}+5 x+1\right)=0 \text {, }
$$
from which $x=-1$ or $x=\frac{-5 \pm \sqrt{21}}{2}$. The largest root is $p=\frac{-5+\sqrt{21}}{2}$, and the smallest is $-q=\frac{-5-\sqrt{21}}{2}$. Then
$$
\frac{p}{q}+\frac{q}{p}=\frac{-5+\sqrt{21}}{-5-\sqrt{21}}+\frac{-5-\sqrt{21}}{-5+\sqrt{21}}=\frac{(-5+\sqrt{21})^{2}+(-5-\sqrt{21})^{2}}{(-5-\sqrt{21})(-5+\sqrt{21})}=\frac{2(25+21)}{4}=23 .
$$ | 23 | Algebra | olympiads | \(\boxed{23}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+5 x+72$. | Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+5 x+72>0 \Leftrightarrow-\frac{1}{3}(x+9)(x-24)>0$, from which $-9<x<24$. On this interval, there are 23 natural values of $x: x=1, x=2, \ldots, x=23$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 7 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers. | 7 | Algebra | olympiads | \(\boxed{7}\) |
2. Find the value of the expression $\frac{a}{b}+\frac{b}{a}$, where $a$ and $b$ are the largest and smallest roots of the equation $x^{3}-9 x^{2}+9 x=1$, respectively. | The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-9\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-9 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-8 x+1\right)=0
$$
from which $x=1$ or $x=4 \pm \sqrt{15}$. The largest root is $a=4+\sqrt{15}$, the smallest is $-b=4-\sqrt{15}$. Then
$$
\frac{a}{b}+\frac{b}{a}=\frac{4+\sqrt{15}}{4-\sqrt{15}}+\frac{4-\sqrt{15}}{4+\sqrt{15}}=\frac{(4+\sqrt{15})^{2}+(4-\sqrt{15})^{2}}{(4+\sqrt{15})(4-\sqrt{15})}=\frac{2(16+15)}{1}=62
$$ | 62 | Algebra | olympiads | \(\boxed{62}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+20 x+63$. | Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+20 x+63>0 \Leftrightarrow-\frac{1}{3}(x+3)(x-63)>0$, from which $-3<x<63$. On this interval, there are 62 natural values of $x: x=1, x=2, \ldots, x=62$. In this case, $y$ takes integer values only when $x$ is divisible by 3 - a total of 20 possibilities. Thus, we get 20 points belonging to the parabola, both of whose coordinates are natural numbers. | 20 | Algebra | olympiads | \(\boxed{20}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{9}+50$. | Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{9}+50>0 \Leftrightarrow x^{2}<450$, from which $-\sqrt{450}<x<\sqrt{450}$. On this interval, there are 21 natural values of $x: x=1, x=2, \ldots, x=21$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 7 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers. | 7 | Algebra | olympiads | \(\boxed{7}\) |
1. Find the number of points in the $x O y$ plane that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{3}+70$. | Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+70>0 \Leftrightarrow x^{2}<210$, from which $-\sqrt{210}<x<\sqrt{210}$. On this interval, there are 14 natural values of $x: x=1, x=2, \ldots, x=14$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 4 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers. | 4 | Algebra | olympiads | \(\boxed{4}\) |
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{9}+33$. | Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{9}+33>0 \Leftrightarrow x^{2}<297$, from which $-\sqrt{297}<x<\sqrt{297}$. On this interval, there are 17 natural values of $x: x=1, x=2, \ldots, x=17$. At the same time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 5 possibilities. Thus, we get 5 points belonging to the parabola, both coordinates of which are natural numbers. | 5 | Algebra | olympiads | \(\boxed{5}\) |
1. Find the number of points in the plane $x O y$ that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{3}+98$ | Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+98>0 \Leftrightarrow x^{2}<294$, from which $-\sqrt{294}<x<\sqrt{294}$. On this interval, there are 17 natural values of $x: x=1, x=2, \ldots, x=17$. At the same time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 5 possibilities. Thus, we get 5 points belonging to the parabola, both coordinates of which are natural numbers. | 5 | Algebra | olympiads | \(\boxed{5}\) |
18. For each natural $n$, which is not a perfect square, the number of values of the variable $x$ is calculated, for which both numbers $x+\sqrt{n}$ and $x^{2}+param1 \cdot \sqrt{n}$ are natural numbers less than param2. Find the total number of such values of $x$.
| param1 | param2 | answer |
| :---: | :---: | :---: |
| 18 | 200 | |
| 20 | 210 | |
| 22 | 250 | |
| 24 | 300 | |
| 26 | 330 | | | For each natural $n$, which is not a perfect square, the number of values of the variable $x$ is calculated, for which both numbers $x+\sqrt{n}$ and $x^{2}+param1 \cdot \sqrt{n}$ are natural numbers less than param2. Find the total number of such values of $x$.
| param1 | param2 | answer |
| :---: | :---: | :---: |
| 18 | 200 | 108 |
| 20 | 210 | 99 |
| 22 | 250 | 117 |
| 24 | 300 | 143 |
| 26 | 330 | 148 | | 108 | Number Theory | olympiads | \(\boxed{108}\) |
4. Find the number of pairs of integers $(x ; y)$ that satisfy the equation $x^{2}+x y=30000000$. | By factoring the left and right sides of the equation, we get $x(x+y)=$ $3 \cdot 2^{7} \cdot 5^{7}$. Then, if $x>0$, $x$ is one of the divisors of the right side. The right side has a total of $2 \cdot 8 \cdot 8=128$ divisors (since any divisor can be represented as $3^{a} \cdot 2^{b} \cdot 5^{c}$, where $a, b$, and $c$ are non-negative integers not exceeding 1, 7, and 7, respectively, i.e., there are 2 ways to choose $a$, 8 ways to choose $b$, and 8 ways to choose $c$). Note that if the right side is divisible by $x$, then it automatically follows that $y \in \mathbb{Z}$, and $y$ is uniquely determined. Therefore, there are a total of $2 \cdot 128=256$ pairs of numbers. | 256 | Algebra | olympiads | \(\boxed{256}\) |
1. It is known that for three consecutive natural values of the argument, the quadratic function $f(x)$ takes the values 6, 14, and 14, respectively. Find the greatest possible value of $f(x)$. | Let $n, n+1, n+2$ be the three given consecutive values of the argument. Since a quadratic function takes the same values at points symmetric with respect to the x-coordinate of the vertex of the parabola $x_{\text{v}}$, then $x_{\text{v}}=n+1.5$, and thus $f(x)$ can be represented as $f(x)=a(x-n-1.5)^{2}+c$. Since $f(n)=6, f(n+1)=14$, we get $\frac{9}{4} a+c=6, \frac{a}{4}+c=14$, from which $a=-4, c=15$. But $c=f\left(x_{\text{v}}\right)$ and is the maximum value of the function. | 15 | Algebra | olympiads | \(\boxed{15}\) |
4. Find the number of pairs of integers $(x ; y)$ that satisfy the equation $y^{2}-x y=700000000$. | Factoring the left and right sides of the equation, we get $y(y-x)=$ $7 \cdot 2^{8} \cdot 5^{8}$. Then if $y>0$, $y$ is one of the divisors of the right side. The right side has a total of $2 \cdot 9 \cdot 9=162$ divisors (since any divisor can be represented as $7^{a} \cdot 2^{b} \cdot 5^{c}$, where $a, b$, and $c$ are non-negative integers not exceeding 1, 8, and 8, respectively, i.e., there are 2 ways to choose $a$, 9 ways to choose $b$, and 9 ways to choose $c$). Note that if the right side is divisible by $y$, then it automatically follows that $x \in \mathbb{Z}$, and in this case, $x$ is uniquely determined. Therefore, there are a total of $2 \cdot 162=324$ pairs of numbers. | 324 | Number Theory | olympiads | \(\boxed{324}\) |
1. Given quadratic trinomials $f_{1}(x)=x^{2}+a x+3, f_{2}(x)=x^{2}+2 x-b, f_{3}(x)=x^{2}+2(a-1) x+b+6$ and $f_{4}(x)=x^{2}+(4-a) x-2 b-3$. Let the differences of their roots be $A, B, C$ and $D$, respectively, and given that $|A| \neq|B|$. Find the ratio $\frac{C^{2}-D^{2}}{A^{2}-B^{2}}$. The values of $A, B, C, D, a, b$ are not specified. | Let $\alpha x^{2}+\beta x+\gamma$ be a quadratic trinomial with a positive discriminant $T$. Then its roots are determined by the formula $x_{1,2}=\frac{-b \pm \sqrt{T}}{2 a}$, so $\left|x_{2}-x_{1}\right|=\left|\frac{-b+\sqrt{T}-(-b-\sqrt{T})}{2 a}\right|=$ $\frac{\sqrt{T}}{|a|} \cdot$ Applying this formula four times, we get
$$
A=\sqrt{a^{2}-12}, B=\sqrt{4+4 b}, C=\sqrt{(2 a-2)^{2}-4(6+b)}, D=\sqrt{(4-a)^{2}+4(2 b+3)}
$$
From this, it follows that $C^{2}-D^{2}=\left(\left(4 a^{2}-8 a-4 b-20\right)-\left(a^{2}-8 a+8 b+28\right)\right)=3\left(a^{2}-4 b-16\right)$, $A^{2}-B^{2}=a^{2}-4 b-16$. Therefore, the desired ratio is 3. | 3 | Algebra | olympiads | \(\boxed{3}\) |
1. Given quadratic trinomials $f_{1}(x)=x^{2}+2 x+a, f_{2}(x)=x^{2}+b x-1, f_{3}(x)=2 x^{2}+(6-b) x+3 a+1$ and $f_{4}(x)=2 x^{2}+(3 b-2) x-a-3$. Let the differences of their roots be $A, B, C$ and $D$, respectively, and given that $|A| \neq|B|$. Find the ratio $\frac{C^{2}-D^{2}}{A^{2}-B^{2}}$. The values of $A, B, C, D, a, b$ are not specified. | Let $\alpha x^{2}+\beta x+\gamma$ be a quadratic trinomial with a positive discriminant $T$. Then its roots are determined by the formula $x_{1,2}=\frac{-b \pm \sqrt{T}}{2 a}$, so $\left|x_{2}-x_{1}\right|=\left|\frac{-b+\sqrt{T}-(-b-\sqrt{T})}{2 a}\right|=$ $\frac{\sqrt{T}}{|a|}$. Applying this formula four times, we get
$$
A=\sqrt{4-4 a}, B=\sqrt{b^{2}+4}, C=\frac{1}{2} \sqrt{(6-b)^{2}-8(1+3 a)}, D=\frac{1}{2} \sqrt{(3 b-2)^{2}+8(a+3)}
$$
From this, it follows that $C^{2}-D^{2}=\frac{1}{4}\left(\left(b^{2}-12 b-24 a+28\right)-\left(9 b^{2}-12 b+8 a+28\right)\right)=-2\left(b^{2}+4 a\right)$, $A^{2}-B^{2}=-\left(b^{2}+4 a\right)$. Therefore, the desired ratio is 2. | 2 | Algebra | olympiads | \(\boxed{2}\) |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 3375. The answer should be presented as an integer. | Since $3375=3^{3} \cdot 5^{3}$, the sought numbers can consist of the following digits: (a) three threes, three fives, and two ones, or (b) one three, one nine, three fives, and three ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then three places out of the remaining five for the fives ( $C_{5}^{3}=\frac{5!}{3!2!}$ ways). Finally, the remaining places are occupied by ones. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{3}=\frac{8!}{3!3!2!}=560$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{3!3!}=1120$.
Finally, we get $560+1120=1680$ ways. | 1680 | Combinatorics | olympiads | \(\boxed{1680}\) |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 16875. The answer should be presented as an integer. | Since $16875=3^{3} \cdot 5^{4}$, the sought numbers can consist of the following digits: (a) three threes, four fives, and one one, or (b) one three, one nine, four fives, and two ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then one place out of the remaining five for the one ( $C_{5}^{1}=5$ ways). Finally, the remaining places are occupied by fives. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{1}=\frac{8!}{3!5!} \cdot 5=280$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{4!2!}=840$. Finally, we get $280+840=1120$ ways. | 1120 | Combinatorics | olympiads | \(\boxed{1120}\) |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 9261. The answer should be presented as an integer. | Since $9261=3^{3} \cdot 7^{3}$, the sought numbers can consist of the following digits: (a) three threes, three sevens, and two ones, or (b) one three, one nine, three sevens, and three ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then three places out of the remaining five for the sevens $\left(C_{5}^{3}=\frac{5!}{3!2!}\right.$ ways). Finally, the remaining places are occupied by ones. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{3}=\frac{8!}{3!3!2!}=560$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{3!3!}=1120$. Finally, we get $560+1120=1680$ ways. | 1680 | Combinatorics | olympiads | \(\boxed{1680}\) |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 64827. The answer should be presented as an integer. | Since $64827=3^{3} \cdot 7^{4}$, the sought numbers can consist of the following digits: (a) three threes, four sevens, and one one, or (b) one three, one nine, four sevens, and two ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then one place out of the remaining five for the one ( $C_{5}^{1}=5$ ways). Finally, the remaining places are occupied by sevens. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{1}=\frac{8!}{3!5!} \cdot 5=280$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{4!2!}=840$.
Finally, we get $280+840=1120$ ways. | 1120 | Combinatorics | olympiads | \(\boxed{1120}\) |
5. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can be repeated) so that the resulting 12-digit number is divisible by 45. In how many ways can this be done | For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by nine, we proceed as follows. We will choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and then select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $2 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=13122$. | 13122 | Number Theory | olympiads | \(\boxed{13122}\) |
5. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 18. In how many ways can this be done? | For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6$ or 8 (5 ways).
To ensure divisibility by nine, we proceed as follows. Choose three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0, 1, 2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that there are $5 \cdot 9 \cdot 9 \cdot 9 \cdot 1 = 3645$ ways. | 3645 | Combinatorics | olympiads | \(\boxed{3645}\) |
5. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 45. In how many ways can this be done? | For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We select three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and choose the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that there are $2 \cdot 9 \cdot 9 \cdot 9 \cdot 1=1458$ ways. | 1458 | Number Theory | olympiads | \(\boxed{1458}\) |
5. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $1,2,3,4,5,6,7,8,9$ (digits can repeat) so that the resulting 12-digit number is divisible by 18. In how many ways can this be done | For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $2, 4, 6$ or 8 (4 ways).
To ensure divisibility by nine, we proceed as follows. We select four digits arbitrarily (this can be done in 9.9 .9 .9 ways), and then choose the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $4 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=26244$. | 26244 | Number Theory | olympiads | \(\boxed{26244}\) |
1. Given quadratic trinomials $f_{1}(x)=x^{2}-a x-3, f_{2}(x)=x^{2}+2 x-b, f_{3}(x)=3 x^{2}+(2-2 a) x-6-b$ and $f_{4}(x)=3 x^{2}+(4-a) x-3-2 b$. Let the differences of their roots be $A, B, C$ and $D$ respectively. It is known that $|C| \neq|D|$. Find the ratio $\frac{A^{2}-B^{2}}{C^{2}-D^{2}}$. The values of $A, B, C, D, a, b$ are not given. | Let $\alpha x^{2}+\beta x+\gamma$ be a quadratic trinomial with a positive discriminant $T$. Then its roots are determined by the formula $x_{1,2}=\frac{-b \pm \sqrt{T}}{2 a}$, so $\left|x_{2}-x_{1}\right|=\left|\frac{-b+\sqrt{T}-(-b-\sqrt{T})}{2 a}\right|=\frac{\sqrt{T}}{|a|}$. Applying this formula four times, we get
$$
A=\sqrt{a^{2}+12}, B=\sqrt{4+4 b}, C=\frac{1}{3} \sqrt{(2-2 a)^{2}+12(6+b)}, D=\frac{1}{3} \sqrt{(4-a)^{2}+12(3+2 b)}
$$
From this, it follows that $C^{2}-D^{2}=\frac{1}{9}\left(\left(4 a^{2}-8 a+12 b+76\right)-\left(a^{2}-8 a+24 b+52\right)\right)=\frac{1}{3}\left(a^{2}-4 b+8\right), A^{2}-$ $B^{2}=a^{2}-4 b+8$. Therefore, the desired ratio is 3. | 3 | Algebra | olympiads | \(\boxed{3}\) |
1. Given quadratic trinomials $f_{1}(x)=x^{2}-2 x+a, f_{2}(x)=x^{2}+b x-2, f_{3}(x)=4 x^{2}+(b-6) x+3 a-2$ and $f_{4}(x)=4 x^{2}+(3 b-2) x-6+a$. Let the differences of their roots be $A, B, C$ and $D$ respectively. It is known that $|C| \neq|D|$. Find the ratio $\frac{A^{2}-B^{2}}{C^{2}-D^{2}}$. The values of $A, B, C, D, a, b$ are not given. | Let $\alpha x^{2}+\beta x+\gamma$ be a quadratic trinomial with a positive discriminant $T$. Then its roots are determined by the formula $x_{1,2}=\frac{-b \pm \sqrt{T}}{2 a}$, so $\left|x_{2}-x_{1}\right|=\left|\frac{-b+\sqrt{T}-(-b-\sqrt{T})}{2 a}\right|=\frac{\sqrt{T}}{|a|}$. Applying this formula four times, we get
$$
A=\sqrt{4-4 a}, B=\sqrt{b^{2}+8}, C=\frac{1}{4} \sqrt{(b-6)^{2}-16(3 a-2)}, D=\frac{1}{4} \sqrt{(3 b-2)^{2}-16(a-6)}
$$
From this, it follows that $C^{2}-D^{2}=\frac{1}{16}\left(\left(b^{2}-48 a-12 b+68\right)-\left(9 b^{2}-16 a-12 b+100\right)\right)=\frac{1}{2}\left(-b^{2}-4 a-4\right)$, $A^{2}-B^{2}=-b^{2}-4 a-4$. Therefore, the desired ratio is 2. | 2 | Algebra | olympiads | \(\boxed{2}\) |
3. On the sides of triangle $A B C$, points were marked: 10 - on side $A B$, 11 - on side $B C$, 12 - on side $A C$. At the same time, none of the vertices of the triangle were marked. How many triangles exist with vertices at the marked points? | Three points out of the 33 given can be chosen in $C_{33}^{3}=5456$ ways. In this case, a triangle is formed in all cases except when all three points lie on one side of the triangle. Thus, $C_{12}^{3}+C_{11}^{3}+C_{10}^{3}=220+165+120=505$ ways do not work. Therefore, there are $5456-505=4951$ triangles. | 4951 | Combinatorics | olympiads | \(\boxed{4951}\) |
3. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 70, 1 \leqslant b \leqslant 50$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5. | The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 14 values of $a$ and 10 values of $b$ that are multiples of 5. Therefore, there are $14 \cdot 50=$ 700 pairs $(a ; b)$ such that $a \vdots 5$ and $10 \cdot 70=700$ pairs such that $b \vdots 5$. Additionally, there are $14 \cdot 10=140$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $700+700-140=1260$. | 1260 | Number Theory | olympiads | \(\boxed{1260}\) |
3. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 80,1 \leqslant b \leqslant 30$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5. | The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 16 values of $a$ and 6 values of $b$ that are multiples of 5. Therefore, there are $16 \cdot 30 = 480$ pairs $(a ; b)$ such that $a \vdots \cdot 5$ and $6 \cdot 80 = 480$ pairs such that $b \vdots 5$. Additionally, there are $16 \cdot 6 = 96$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $480 + 480 - 96 = 864$. | 864 | Number Theory | olympiads | \(\boxed{864}\) |
8. For each natural $n$, which is not a perfect square, all values of the variable $x$ are calculated for which both numbers $x+\sqrt{n}$ and $x^{3}+$ param1 $\sqrt{n}$ are integers. Find the total number of such values of $x$.
| param1 | answer |
| :---: | :---: |
| 1524 | |
| 1372 | |
| 1228 | |
| 1092 | |
| 964 | | | For each natural $n$, which is not a perfect square, all values of the variable $x$ are calculated for which both numbers $x+\sqrt{n}$ and $x^{3}+$ param1 $\sqrt{n}$ are integers. Find the total number of such values of $x$.
| param1 | answer |
| :---: | :---: |
| 1524 | 39 |
| 1372 | 33 |
| 1228 | 35 |
| 1092 | 27 |
| 964 | 29 | | 33 | Algebra | olympiads | \(\boxed{33}\) |
1. Nils has a goose farm. Nils calculated that if he sells 75 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 15 days earlier than if he doesn't make such a purchase. How many geese does Nils have? | Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-75)=(k-15) x(n+100) \\
k n=(k+20)(n-75)=(k-15)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=60, n=300$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points. | 300 | Algebra | olympiads | \(\boxed{300}\) |
1. Nils has a goose farm. Nils calculated that if he sells 50 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 10 days earlier than if he doesn't make such a purchase. How many geese does Nils have? | Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-50)=(k-10) x(n+100) \\
k n=(k+20)(n-50)=(k-10)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=20, n=100$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points. | 300 | Algebra | olympiads | \(\boxed{300}\) |
# Problem No. 6 (10 points)
The density of a body is defined as the ratio of its mass to the volume it occupies. A homogeneous cube with a volume of \( V = 8 \, \text{m}^3 \) is given. As a result of heating, each of its edges increased by 4 mm. By what percentage did the density of this cube change?
Answer: decreased by \( 6 \% \) | # Solution and evaluation criteria:
Volume of the cube: $v=a^{3}$, where $a$ is the length of the edge, therefore:
$a=2 \partial m=200 mm$.
Final edge length: $a_{\kappa}=204$ mm.
Thus, the final volume: $V_{\kappa}=a_{K}^{3}=2.04^{3}=8.489664 \partial \mu^{3} \approx 1.06 V$.
Therefore, the density:
$\rho_{K}=\frac{m}{V_{K}}=\frac{m}{1.06 V}=0.94 \frac{m}{V} \approx 0.94 \rho$. The density has decreased by approximately $6 \%$. | 6 | Algebra | olympiads | \(\boxed{6}\) |
# Problem №2 (10 points)
There are two cubes. The mass of the second is $25 \%$ less than the mass of the first, and the edge length of the second cube is $25 \%$ greater than that of the first. By what percentage does the density of the second cube differ from the density of the first?
# | # Solution:
Volume of the second cube
$V=a^{3}=(1.25 a)^{3}$
(4 points)
And its density:
$\rho=\frac{m}{V}=\frac{0.75 m}{(1.25 a)^{3}}=0.384 \frac{m}{a^{3}}$.
(4 points)
That is, the density of the second cube is less than that of the first by $61.6 \%$
(2 points)
# | 61.6 | Algebra | olympiads | \(\boxed{61.6}\) |
3. Nils has a goose farm. Nils calculated that if he sells 75 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 15 days earlier than if he doesn't make such a purchase. How many geese does Nils have? | Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-75)=(k-15) x(n+100) \\
k n=(k+20)(n-75)=(k-15)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=60, n=300$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points. | 300 | Algebra | olympiads | \(\boxed{300}\) |
3. Nils has a goose farm. Nils calculated that if he sells 50 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 10 days earlier than if he doesn't make such a purchase. How many geese does Nils have? | Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-50)=(k-10) x(n+100) \\
k n=(k+20)(n-50)=(k-10)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=20, n=100$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points. | 300 | Algebra | olympiads | \(\boxed{300}\) |
2. Let
$$
\sqrt{49-a^{2}}-\sqrt{25-a^{2}}=3
$$
Calculate the value of the expression
$$
\sqrt{49-a^{2}}+\sqrt{25-a^{2}} .
$$ | Let
$$
\sqrt{49-a^{2}}+\sqrt{25-a^{2}}=x
$$
Multiplying this equality by the original one, we get $24=3x$.
Evaluation. Full solution: 11 points. | 8 | Algebra | olympiads | \(\boxed{8}\) |
2. The sequence $\left(a_{n}\right)$ is defined by the following relations: $a_{1}=1, a_{2}=2, a_{n}=a_{n-1}-a_{n-2}+n$ (for $n \geqslant 3$). Find $a_{2019}$. | Let's list the first terms of the sequence:
$$
1,2,4,6,7,7,7,8,10,12,13,13,13,14,16,18,19,19,19,20,21,23, \ldots
$$
We can observe a pattern: $a_{n+6}=a_{n}+6$. Let's prove it. We have
$a_{n+1}=a_{n}-a_{n-1}+n+1=\left(a_{n-1}-a_{n-2}+n\right)-a_{n-1}+n+1=-a_{n-2}+2 n+1$.
By substituting $n$ with $n+2$ in the obtained equation, we get
$$
a_{n+3}=-a_{n}+2(n+2)+1=-a_{n}+2 n+5 .
$$
Now, let's substitute $n$ with $n+3$:
$$
a_{n+6}=-a_{n+3}+2(n+3)+5=a_{n}-2 n-5+2(n+3)+5=a_{n}+6
$$
Now it's easy to find the answer:
$$
a_{2019}=a_{3+6 \cdot 336}=a_{3}+6 \cdot 636=4+6 \cdot 636=2020
$$
Evaluation. 12 points for a complete solution. If the pattern is noticed but not proven, then (with the correct answer) 6 points. | 2020 | Algebra | olympiads | \(\boxed{2020}\) |
2. The sequence $\left(a_{n}\right)$ is defined by the following relations: $a_{1}=1, a_{2}=3, a_{n}=a_{n-1}-a_{n-2}+n$ (for $n \geqslant 3$). Find $a_{1000}$. | Let's list the first terms of the sequence:
$$
1,3,5,6,6,6,7,9,11,12,12,12,13,15,17,18,18,18,19,21, \ldots
$$
We can see a pattern: $a_{n+6}=a_{n}+6$. Let's prove it. We have
$a_{n+1}=a_{n}-a_{n-1}+n+1=\left(a_{n-1}-a_{n-2}+n\right)-a_{n-1}+n+1=-a_{n-2}+2 n+1$.
By substituting $n$ with $n+2$ in the obtained equation, we get
$$
a_{n+3}=-a_{n}+2(n+2)+1=-a_{n}+2 n+5 .
$$
Now, let's substitute $n$ with $n+3$:
$$
a_{n+6}=-a_{n+3}+2(n+3)+5=a_{n}-2 n-5+2(n+3)+5=a_{n}+6
$$
Now it's easy to find the answer:
$$
a_{1000}=a_{4+6 \cdot 166}=a_{4}+6 \cdot 166=6+6 \cdot 166=1002
$$
Evaluation. Full solution is worth 12 points. If the pattern is noticed but not proven, then (with the correct answer) 6 points. | 1002 | Algebra | olympiads | \(\boxed{1002}\) |
1. (17 points) The price of an entry ticket to the stadium is 400 p. After reducing the entry fee, the number of spectators increased by $25 \%$, and the revenue increased by $12.5 \%$. What is the new price of the entry ticket after the price reduction? | Let the number of viewers before the ticket price reduction be 1 person. Then the revenue was 400 rubles. Let $x$ rubles be the new ticket price. We get the equation $x \cdot 1.25 = 400 - 1.125$. From which $x = 360$. | 360 | Algebra | olympiads | \(\boxed{360}\) |
1. (17 points) The price of an entry ticket to the stadium is 400 p. After increasing the entry fee, the number of spectators decreased by $20 \%$, but the revenue increased by $5 \%$. What is the new price of the entry ticket after the price increase? | Let the number of viewers before the ticket price reduction be 1 person. Then the revenue was 400 rubles. Let $x$ rubles be the new ticket price. We get the equation $x \cdot 0.8 = 400 \cdot 1.05$. From which $x=525$. | 525 | Algebra | olympiads | \(\boxed{525}\) |
2. (17 points) A tourist travels from point $A$ to point $B$ in 2 hours and 14 minutes. The route from $A$ to $B$ goes uphill first, then on flat terrain, and finally downhill. What is the length of the uphill road if the tourist's speed downhill is 6 km/h, uphill is 4 km/h, and on flat terrain is 5 km/h, and the total distance between $A$ and $B$ is 10 km? Additionally, the distances uphill and on flat terrain are whole numbers of kilometers. | Let $x$ km be the distance the tourist walks uphill, $y$ km - on flat ground, then $10-x-y$ km - downhill. We get $\frac{x}{4}+\frac{y}{5}+\frac{10-x-y}{6}=\frac{67}{30}$. After transformations, $5 x+2 y=34$. It is obvious that $x$ must be even and $x+y \leq 10$. The only solution is $x=6, y=2$. | 6 | Algebra | olympiads | \(\boxed{6}\) |
4. (20 points) An aluminum and a copper part have the same volume. The density of aluminum $\rho_{A}=2700 \mathrm{kg} / \mathrm{m}^{3}$, the density of copper $\rho_{M}=8900 \mathrm{kg} / \mathrm{m}^{3}$. Find the mass of copper, if it is known that the masses of the parts differ by $\Delta m=60 \mathrm{g}$. | Volume of aluminum: $V=\frac{m_{M}-\Delta m}{\rho_{A}}$, volume of copper: $V=\frac{m_{M}}{\rho_{M}}$. We get: $\frac{m_{M}}{\rho_{M}}=\frac{m_{M}-\Delta m}{\rho_{A}} . \quad$ From this, the mass of aluminum: $m_{A}=\frac{\Delta m \cdot \rho_{M}}{\rho_{M}-\rho_{A}}=\frac{0.06 \cdot 8900}{8900-2700} \approx 0.086 \kappa 2 \approx 86 g$. | 862 | Algebra | olympiads | \(\boxed{862}\) |
2. (17 points) Find the smallest root of the equation
$$
\sqrt{x+2}+2 \sqrt{x-1}+3 \sqrt{3 x-2}=10
$$ | It is clear that 2 is a root of the equation. The function on the left side of the equation is increasing (as the sum of increasing functions). Therefore, there are no other roots. | 2 | Algebra | olympiads | \(\boxed{2}\) |
2. (17 points) Find the largest root of the equation
$$
3 \sqrt{x-2}+2 \sqrt{2 x+3}+\sqrt{x+1}=11
$$ | It is clear that 3 is a root of the equation. The function on the left side of the equation is increasing (as the sum of increasing functions). Therefore, there are no other roots. | 3 | Algebra | olympiads | \(\boxed{3}\) |
# Problem №1 (15 points)
Two identical cars are driving in the same direction. The speed of one is $36 \kappa \mu / h$, and the other is catching up at a speed of $54 \mathrm{km} / h$. It is known that the reaction time of the driver of the rear car to the activation of the brake lights of the front car is 2 seconds. What should be the distance between the cars so that they do not collide if the first driver decides to brake sharply? For a car of this make, the braking distance is 40 meters at a speed of $72 \kappa \mu / h$. | # Solution:
Convert all speeds to SI units:
$36 \kappa m / h = 10 m / s$
$54 \kappa m / h = 15 m / s$
$72 \kappa m / h = 20 m / s$
The acceleration of a car of this make:
$a=\frac{v^{2}}{2 S}=\frac{20^{2}}{2 \cdot 40}=5 \mathrm{M} / s^{2}$
Distance traveled by the first car before stopping:
$S_{1}=\frac{v_{2}^{2}}{2 a}=\frac{10^{2}}{2 \cdot 5}=10 \mathrm{M}$
Distance traveled by the second car before stopping:
$S_{2}=v_{2} \cdot 2+\frac{v_{2}^{2}}{2 a}=15 \cdot 2+\frac{15^{2}}{2 \cdot 5}=30+22.5=52.5 \mathrm{M}$
Therefore, the distance between the cars should be no less than:
$l=S_{2}-S_{1}=52.5-10=42.5$ meters
(3 points) | 42.5 | Algebra | olympiads | \(\boxed{42.5}\) |
# Problem №3 (10 points)
The circuit diagram shown is composed of identical resistors. If point $A$ is connected to point $C$, and point $B$ is connected to point $D$, the resistance of the circuit changes by 10 Ohms. Determine the resistance of one resistor. The connections between points were made using zero-resistance jumpers.
 | # Solution:
If the resistance of one resistor is $R$, then the initial total resistance of the series connection is $3 R$
After the jumpers were activated, we get a parallel connection of three resistors.
In this case, their total resistance is $\frac{R}{3}$
According to the condition: $3 R-\frac{R}{3}=10$
Final result: $R=3.75$ Ohms
# | 3.75 | Algebra | olympiads | \(\boxed{3.75}\) |
4. Let $a, b, c, d, e$ be positive integers. Their sum is 2018. Let $M=\max (a+b, b+c, c+d, d+e)$. Find the smallest possible value of $M$. | Estimation. We have the inequalities
$$
a+b \leqslant M ; \quad b+c \leqslant M ; \quad c+d \leqslant M ; \quad d+e \leqslant M
$$
Multiply the first and last inequalities by 2 and add the other two. We get:
$$
2(a+b+c+d+e)+b+d \leqslant 6 M ; \quad 6 M \geqslant 4036+b+d \geqslant 4038 ; \quad M \geqslant 673 .
$$
Example. The equality $M=673$ is achieved when $a=c=e=672$, $b=d=1$.
Evaluation. 14 points for a correct solution. If there is only a correct example, 7 points.
## Multidisciplinary Engineering Olympiad "Star" in Natural Sciences Final Stage 2017-2018 academic year Problems, answers, and evaluation criteria 9th grade Variant 1 physics | 673 | Algebra | olympiads | \(\boxed{673}\) |
4. Let $a, b, c, d, e$ be positive integers. Their sum is 2345. Let $M=\max (a+b, b+c, c+d, d+e)$. Find the smallest possible value of $M$. | Estimation. We have the inequalities
$$
a+b \leqslant M ; \quad b+c \leqslant M ; \quad c+d \leqslant M ; \quad d+e \leqslant M
$$
Multiply the first and last inequalities by 2 and add the other two. We get:
$2(a+b+c+d+e)+b+d \leqslant 6 M ; \quad 6 M \geqslant 4690+b+d \geqslant 4692 ; \quad M \geqslant 782$.
Example. The equality $M=782$ is achieved when $a=c=e=781$, $b=d=1$.
Evaluation. 14 points for a correct solution. If there is only a correct example, 7 points.
## Multidisciplinary Engineering Olympiad "Star" in Natural Sciences Final Stage 2017-2018 academic year Problems, answers, and evaluation criteria 9th grade Variant 2 physics | 782 | Algebra | olympiads | \(\boxed{782}\) |
3. In the cells of a $3 \times 3$ square, the numbers $1,2,3, \ldots, 9$ are arranged. It is known that any two consecutive numbers are located in adjacent (by side) cells. Which number can be in the central cell if the sum of the numbers in the corner cells is $18?$ | Let's color the cells in a checkerboard pattern: suppose the corner and central cells are black, and the rest are white. From the condition, it follows that in cells of different colors, the numbers have different parities. Since there are five black cells and four white cells, we get that the odd numbers are in the black cells. Their total sum is $1+3+5+7+9=$ 25. Therefore, the number in the central cell is $7=25-18$.
Evaluation. 12 points for a correct solution. If an example of the arrangement of numbers satisfying the problem's condition is provided but the uniqueness of the answer is not proven, 6 points. | 7 | Logic and Puzzles | olympiads | \(\boxed{7}\) |
8. A cube consists of eight smaller identical cubes. Two of the smaller cubes were replaced with ones of the same size but with a density twice as high. Determine the ratio of the initial and final densities of the large cube. (10 points) | The relationship between mass and volume: $m=\rho V$ (2 points), that is, the new cubes, with the same volume, are twice as heavy. Initial density: $\rho_{\text {initial }}=\frac{8 m_{0}}{8 V_{0}} \quad$ (3 points).
Final density: $\quad \rho_{\text {final }}=\frac{6 m_{0}+2 m_{1}}{8 V_{0}}=\frac{6 m_{0}+2 \cdot 2 m_{0}}{8 V_{0}}=\frac{10 m_{0}}{8 V_{0}} \quad(3$ points $)$.
Final result: $\frac{\rho_{\text {initial }}}{\rho_{\text {final }}}=\frac{8}{10}=0.8$ (2 points).
## Final Stage
$2017-2018$ academic year
## Tasks, answers, and evaluation criteria 7th grade Variant II h วłf Ћ วłGr ə | 0.8 | Algebra | olympiads | \(\boxed{0.8}\) |
3. In the cells of a $3 \times 3$ square, the numbers $0,1,2, \ldots, 8$ are arranged. It is known that any two consecutive numbers are located in adjacent (by side) cells. Which number can be in the central cell if the sum of the numbers in the corner cells is $18?$ | Let's color the cells in a checkerboard pattern: suppose the corner and central cells are black, and the rest are white. From the condition, it follows that in cells of different colors, the numbers have different parities. Since there are five black cells and four white cells, we get that the even numbers are in the black cells. Their total sum is $0+2+4+6+8=20$. Therefore, the number in the central cell is $2=20-18$.
Evaluation. 12 points for a correct solution. If an example of the arrangement of numbers satisfying the problem's condition is provided but the uniqueness of the answer is not proven, 6 points. | 2 | Logic and Puzzles | olympiads | \(\boxed{2}\) |
8. A cube consists of eight smaller identical cubes. Three of the smaller cubes were replaced with ones of the same size but with a density three times greater. Determine the ratio of the final to the initial density of the large cube. (10 points) | The relationship between mass and volume: $m=\rho V$ (2 points), that is, the new cubes, with the same volume, are three times heavier. Initial density: $\rho_{\text {initial }}=\frac{8 m_{0}}{8 V_{0}}$
(3 points). Final density: $\rho_{\text {final }}=\frac{5 m_{0}+3 m_{1}}{8 V_{0}}=\frac{5 m_{0}+3 \cdot 3 m_{0}}{8 V_{0}}=\frac{14 m_{0}}{8 V_{0}}$ (3 points).
Final result: $\frac{\rho_{\text {final }}}{\rho_{\text {initial }}}=\frac{14}{8}=1.75$ (2 points). | 1.75 | Algebra | olympiads | \(\boxed{1.75}\) |
2. The teacher wrote a positive number $x$ on the board and asked Kolya, Petya, and Vasya to raise this number to the 3rd, 4th, and 12th power, respectively. It turned out that Kolya's number has at least 9 digits before the decimal point, and Petya's number has no more than 11 digits before the decimal point. How many digits are there before the decimal point in Vasya's number? | From the condition, it follows that $x^{3} \geqslant 10^{8}$, and $x^{4}<10^{11}$. Therefore, $10^{32} \leqslant x^{12}<10^{33}$. This means that the integer part of Vasya's number is a 33-digit number.
Evaluation. 13 points for the correct solution. | 33 | Number Theory | olympiads | \(\boxed{33}\) |
2. The teacher wrote a positive number $x$ on the board and asked Kolya, Petya, and Vasya to raise this number to the 4th, 5th, and 20th power, respectively. It turned out that Kolya's number has at least 8 digits before the decimal point, and Petya's number has no more than 9 digits before the decimal point. How many digits are there before the decimal point in Vasya's number? | From the condition, it follows that $x^{4} \geqslant 10^{7}$, and $x^{5}<10^{9}$. Therefore, $10^{35} \leqslant x^{20}<10^{36}$. This means that the integer part of Vasya's number is a 36-digit number.
Evaluation. 13 points for the correct solution. | 36 | Number Theory | olympiads | \(\boxed{36}\) |
1. (17 points) Three cyclists, Dima, Misha, and Petya, started a 1 km race simultaneously. At the moment Misha finished, Dima still had to cover one tenth of the distance, and at the moment Dima finished, Petya still had to cover one tenth of the distance. How far apart (in meters) were Petya and Dima when Misha finished? (The cyclists are riding at constant speeds). | Let $v_{1}$ be the speed of Misha, $v_{2}$ be the speed of Dima, and $v_{3}$ be the speed of Petya. Then $v_{2}=0.9 v_{1}$, since in the same amount of time Misha traveled 1000 m, while Dima traveled 900 m, and $v_{3}=0.9 v_{2}$, since in the same amount of time Dima traveled 1000 m, while Petya traveled 900 m. Since $v_{3}=$ $0.9 \cdot 0.9 v_{1}=0.81 v_{1}$, at the moment Misha finished, Petya had traveled 810 meters. The distance between Petya and Dima: $900-810=90$. | 90 | Algebra | olympiads | \(\boxed{90}\) |
3. (16 points) In a class, some students study only English, some study only German, and some study both languages. What percentage of the class studies both languages if 90% of all students study English and 80% study German? | From the condition, it follows that $10 \%$ do not study English and $20 \%$ do not study German. Therefore, $10 \%+20 \%=30 \%$ study only one language, and the remaining $70 \%$ study both languages. | 70 | Combinatorics | olympiads | \(\boxed{70}\) |
End of preview. Expand
in Data Studio
README.md exists but content is empty.
- Downloads last month
- 19